Lorsqu'on cherche à déterminer les propriétés d'un corps pur, l'une des premières difficultés réside dans le choix d'une équation d'état. On sait en effet que le modèle des gaz idéaux est caractérisé, en variables molaires, par la loi : Pv = RT

Cette loi n'est valable que loin de la courbe d'équilibre liquide-vapeur, pour des valeurs de la pression faibles, ou de la température élevées. Plus on se rapproche de la courbe de saturation, plus l'hypothèse que la capacité thermique Cp du corps est indépendante de la pression devient fausse. Pour déterminer l'état d'un fluide réel, on utilise le plus souvent un diagramme thermodynamique, un tableau de valeurs des propriétés thermodynamiques, ou encore un jeu d'équations d'état^[1] couvrant les diverses zones nécessaires.

De nombreuses équations d'état^[1] ont été proposées et continuent d'être mises au point. Parmi les plus utilisées on trouve les équations cubiques, présentées ci-dessous.

Si l'on fait abstraction du modèle des gaz parfaits, qui ne permet pas de représenter les gaz réels, les modèles les plus simples sont les cubiques, qui, à partir d'un petit nombre de variables caractéristiques du fluide (masse molaire, coordonnées critiques, facteur acentrique, etc.), fournissent des résultats généralement bons dans la zone vapeur, mais moins précis en zone liquide, notamment pour le calcul du volume (ou de la densité).

Le grand intérêt des cubiques est qu'elles peuvent être résolues formellement, ce qui simplifie considérablement le calcul des propriétés thermodynamiques des fluides. Leur pouvoir prédictif reste cependant limité.

Les cubiques sont pour la plupart dérivées de l'équation d'état développée à l'origine par Van der Waals, qui comprend un terme représentant les forces d'attraction et un terme représentant les interactions répulsives basé sur le modèle de sphère dure.

Les autres cubiques, développées en améliorant à chaque fois ce terme répulsif, ne sont applicables que pour des molécules supposées sphériques et ne s'associant pas entre elles. On ne peut donc pas en toute rigueur les utiliser pour représenter un fluide dont les molécules sont fortement non sphériques ou qui peuvent s'associer.

L'une des cubiques les plus simples est celle de Redlich-Kwong qui s'écrit :

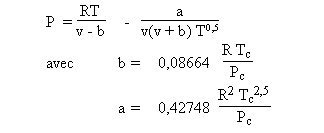
Ne nécessitant que la connaissance des coordonnées critiques du fluide, elle est très générale, mais ne s'applique pas à tous les fluides avec la même précision.

Diverses variantes utilisant une caractéristique supplémentaire du fluide, le facteur acentrique omega, ont été proposées dans la littérature (Wilson, Soave, Peng Robinson...).

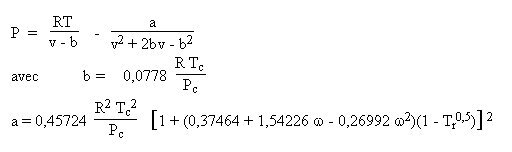
Pour illustrer l'importance du choix de l'équation d'état, nous utiliserons le progiciel PE 2000 (PE signifie Phase Equilibria), développé par l'équipe du Professor Brunner de l'Université Technique de Hambourg-Harbourg. PE 2000 est un outil permettant de corréler des équations d'équilibre de phase avec des données expérimentales. C'est un progiciel disponible gratuitement sur Internet .

PE 2000 peut déterminer les paramètres des équations d'état^[1] pour les corps purs sur la base des pressions et des densités molaires de vapeur dans les conditions de saturation. Des fonctions graphiques permettent une comparaison visuelle des données expérimentales et calculées de la courbe de pression de vapeur et des données PvT.

En corrélant les équilibres de phase liés aux processus d'extraction de gaz, il est possible, pendant l'optimisation des paramètres des équations d'état^[1] pour les corps purs, d'imposer le respect de la température et de la pression critiques du solvant supercritique.

PE 2000 permet de reproduire le comportement de phase des systèmes binaires et ternaires, en déterminant, pour chaque équation d'état, les paramètres binaires d'interaction optimaux correspondant à un ensemble donné de règles de mélange. De plus, pour un jeu de paramètres d'interaction donné, PE 2000 offre la possibilité de calculer les équilibres de phase et les densités molaires dans toutes les conditions.

Si l'on dispose de valeurs de référence, soit expérimentales, soit issues de la littérature, le progiciel PE 2000 permet ainsi d' ajuster les paramètres de différentes équations d'état^[1] ou les coefficients d'interaction.

Les figures ci-dessous représentent le diagramme (pression/densité molaire) de l'ammoniac, obtenu avec deux équations d'état^[1] dont les paramètres ont été optimisés par PE 2000 par rapport aux données expérimentales disponibles, représentées par les points. Sur ces diagrammes, on a fait apparaître quatre isothermes, correspondant aux températures 323 K, 373 K, 423 K et 473 K.

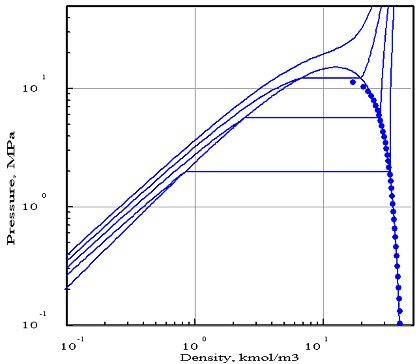
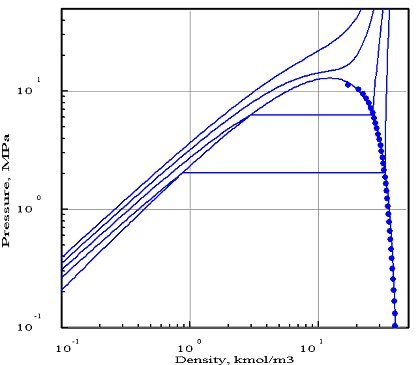
Le premier diagramme correspond à l'équation de Redlich-Kwong, et le second à celle de Peng-Robinson. Comme on peut le voir, cette dernière donne un bien meilleur ajustement. En particulier, l'isotherme 423 K coupe la courbe de saturation , alors que la température critique de l'ammoniac est égale à 405,65 K.

L'équation de Redlich-Kwong, qui ne comporte que deux paramètres (en théorie, la pression et la température critiques, mais l'optimisation par rapport aux données expérimentales a conduit dans ce cas à introduire des valeurs pseudo-critiques qui diffèrent des valeurs réelles), se révèle beaucoup moins précise que celle de Peng Robinson qui utilise un troisième paramètre, le facteur acentrique. Généralement, un plus grand nombre de paramètres permet d'obtenir une meilleure précision, mais ce n'est toutefois pas toujours vrai.

Cet exemple montre l'importance d'une part de bien choisir l'équation d'état, et d'autre part d' effectuer des comparaisons avec les données de référence disponibles, si possible expérimentales.

Il est fréquent qu'une seule équation d'état ne permette pas d'obtenir un bon accord avec les données expérimentales dans toutes les zones d'utilisation du progiciel. A titre d'exemple, la figure ci-dessous montre le résultat de l'optimisation par PE 2000 du calage d'une équation de Peng Robinson pour l'eau.

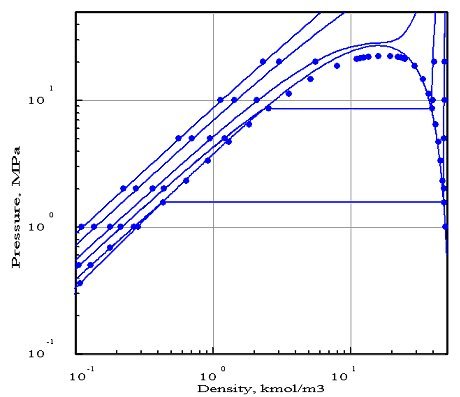
Les isothermes correspondent ici aux températures 373 K, 473 K, 573 K, 673 K et 873 K. L'accord avec les données expérimentales est à peu près bon, sauf pour la courbe d'équilibre liquide-vapeur au dessus de 10 MPa (100 bars).

Ces exemples ont indirectement montré que les cubiques ne permettent pas toujours de bien représenter certains fluides. C'est particulièrement le cas de ceux dont les molécules ne sont pas sphériques ou qui comportent des liaisons hydrogène. De nouvelles équations d'état ont été proposées récemment pour ces types de fluides, comme l'équation Cubic Plus Association (CPA), qui ajoute des termes complémentaires à l'équation d'une cubique, et la famille d'équations Statistical Associating Fluid Theory (SAFT). Une page du portail leur est dédiée.