Diagrammes utilisés pour les cycles de réfrigération à absorption
Les cycles à absorption liquide mettent en jeu au moins deux fluides : un solvant et un soluté (le réfrigérant).
Bien que d'autres couples soient étudiés, les seuls qui soient utilisés en pratique pour la quasi-totalité des applications sont les deux couples LiBr-H2O et NH3-H2O.
Parmi les conditions requises pour que le couple pressenti soit approprié, il faut d'une part que le solvant ait une grande affinité vis à vis du soluté, et d'autre part que ce dernier soit beaucoup plus volatil que le solvant, afin que la séparation des deux constituants soit la meilleure possible.
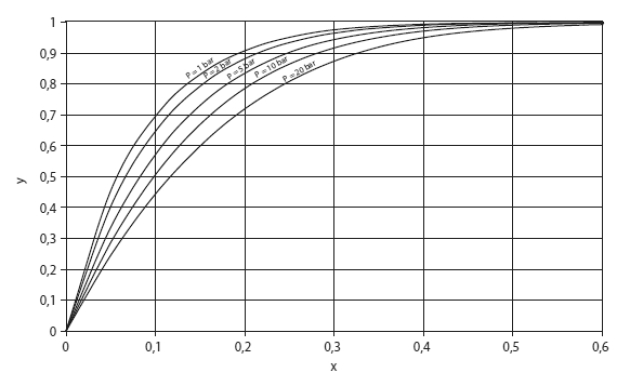
La courbe figure ci-dessous visualise, pour le couple eau-ammoniac, la relation existant entre la fraction massique de liquide et celle de la vapeur d'ammoniac, pour différentes pressions (1, 2, 5, 10 et 20 bar). Elle montre clairement que, dès lors que la fraction massique liquide du soluté x dépasse 0,4, la teneur en ammoniac de la vapeur dépasse 0,95.
Pour le mélange bromure de lithium-eau, la séparation est encore plus nette, au point que l'on peut légitimement supposer que la vapeur d'eau est pure.
Avec le couple LiBr-H2O, l'eau est le réfrigérant, ce qui impose deux contraintes : d'une part les pressions de travail sont très basses compte tenu de la loi de pression saturante de l'eau, et d'autre part la température minimale du cycle doit être supérieure à 0 °C. Les machines utilisant le couple bromure de lithium-eau ne sont utilisées qu'en conditionnement d'air.
La manière dont peuvent être calculées dans le cas général les propriétés d'un mélange de deux fluides réels est présentée dans cette page.
Pour les calculs des cycles à absorption liquide, même si on utilise généralement des équations spécifiques comme nous le verrons ci-dessous, les phénomènes physiques sont de même nature, de telle sorte que cette présentation conserve sa pertinence.
Diagramme de Oldham
Le diagramme de Oldham (Figure ci-dessous) permet de visualiser les courbes de pression saturante du mélange considéré, pour différentes valeurs de sa composition (en fraction massique du soluté ou du solvant selon les cas).
La pression apparaît en ordonnée, avec une échelle logarithmique, tandis que les abscisses correspondent à la température de bulle Tb.
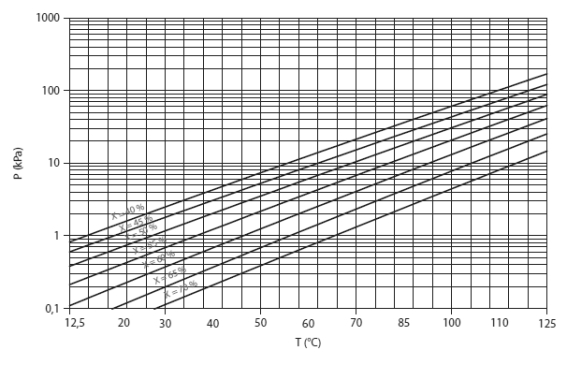
Si l'on choisit (-1/Tb) pour l'échelle des températures, les isotitres sont très proches de droites. Les extrêmes correspondent à l'équilibre liquide-vapeur des corps purs. Une évolution de la solution riche ou de la solution pauvre correspond donc à un segment de droite incliné parallèle à l'isotitre la plus proche. L'allure générale proche d'un parallélogramme des cycles dans ce diagramme a ainsi conduit les scientifiques du domaine à schématiser les architectures de leurs machines sous forme de losange.
Dans les machines utilisant le mélange LiBr-H2O, la différence de tension de vapeur du solvant (LiBr) et du soluté (H2O) est telle que l'on peut négliger la fraction massique du solvant en phase vapeur, ce qui permet de simplifier les calculs : le diagramme d'équilibre peut alors être directement gradué en fonction de la température de la solution.
Équations du couple LiBr-H2O
Pour le couple LiBr-H2O, l'ASHRAE propose les équations (6.6) et (6.7), établies en généralisant au mélange la loi de tension saturante du réfrigérant (l'eau), dans laquelle la température de l'eau t' (°C) est remplacée par une fonction linéaire de la température de la solution t (°C). P, exprimée à partir du logarithme décimal, est la pression en kPa, et X la fraction massique du mélange en LiBr.
Ces équations, qui ont servi à établir le diagramme de la figure ci-dessus, sont valables dans les intervalles de valeurs suivantes :
-15 < t' < 110 °C, 5 < t < 175 °C, 45 < X < 70 %.
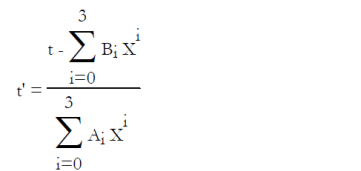
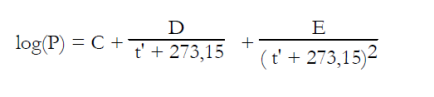
A0 | -2,00755 | B0 | 124,937 | C | 7,05 |
A1 | 0,16976 | B1 | -7,71649 | D | -1596,49 |
A2 | -3,13E-03 | B2 | 0,152286 | E | -104095,5 |
A3 | 1,98E-05 | B3 | -7,95E-04 |
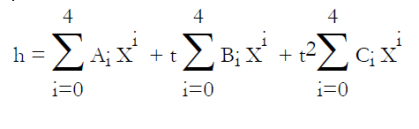
A0 | -2024,33 | B0 | 18,2829 | C0 | -0,03700821 |
A1 | 163,309 | B1 | -1,1691757 | C1 | 2,89E-03 |
A2 | -4,88161 | B2 | 0,03248041 | C2 | -8,13E-05 |
A3 | 0,06302948 | B3 | -4,03E-04 | C3 | 9,91E-07 |
A4 | -2,91E-04 | B4 | 1,85E-06 | C4 | -4,44E-09 |
Ce mélange est disponible dans la modélothèque.
Diagramme de Merkel
Le diagramme de Oldham est facile à comprendre et à utiliser comme on le verra plus loin, mais, tout comme les lentilles d'équilibre isobares ou isothermes, il présente l'inconvénient de ne fournir aucune information sur les énergies mises en jeu.
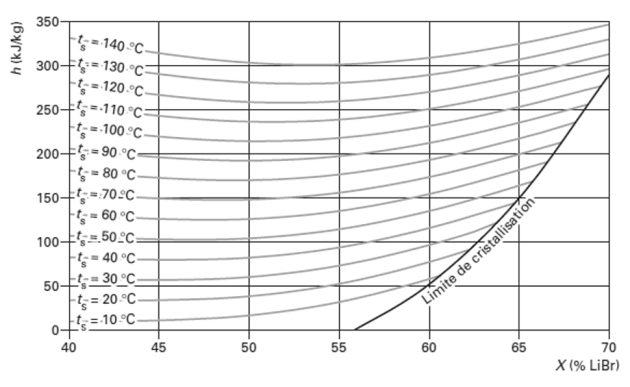
Le diagramme de Merkel (ou diagramme enthalpie-concentration) est quant à lui construit avec l'enthalpie comme ordonnée, et la fraction massique du soluté (ou souvent du solvant pour le couple LiBr-H2O) en abscisse. Il permet ainsi de superposer les informations de plusieurs lentilles d'équilibre isobares tout en faisant apparaître les enthalpies. On trouvera ci-dessous le diagramme de Merkel du mélange ammoniac-eau.
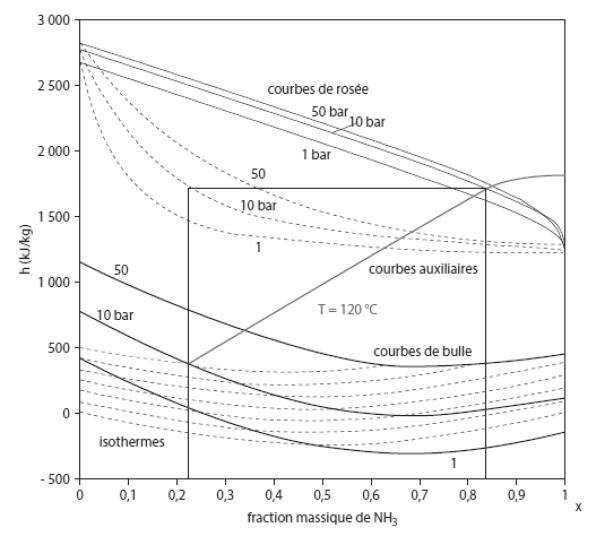
Il comprend cinq types de courbes :
un faisceau de courbes de bulle à P = Cste, en traits continus à concavité tournée vers le haut ;
un faisceau de courbes de rosée pour les mêmes pressions, en traits continus à concavité tournée vers le bas ;
un faisceau d'isothermes en zone liquide, en traits pointillés dans la partie basse du diagramme, valable quelle que soit la pression, l'influence de la pression sur l'enthalpie du liquide étant en première approximation négligeable (à titre d'exemple, l'écart d'enthalpie de la solution liquide à 30 % d'ammoniac en masse varie à 0 °C de 5 kJ/kg lorsque la pression passe de 0,5 à 50 bar, tandis que la partie utile du diagramme couvre plus de 1000 kJ/kg dans la zone liquide) ;
un ensemble de courbes dites auxiliaires ou de construction, en traits pointillés dans la partie haute du diagramme, qui permet, pour une pression donnée, connaissant la fraction massique en soluté du liquide x, de déterminer la fraction massique en soluté de la vapeur y ;
un faisceau d'isotitres en frigorigène de la phase vapeur, qui permet, pour une pression donnée, de connaître la fraction massique en liquide correspondant à l'isotitre vapeur choisi (ce dernier ensemble de courbes est parfois omis du diagramme de Merkel, comme sur cet exemple).
En revanche, on ne fait pas apparaître dans le diagramme de Merkel les isothermes dans la zone vapeur, car elles dépendent de la pression et le diagramme deviendrait illisible.
Références
ASHRAE, Fundamentals Handbook (SI), Thermophysical properties of refrigerants, 2001.
Ziegler B., Trepp Ch., Equation of state for ammonia-water mixtures, Revue Internationale du Froid, Vol. 7, Number 2, Butterworth, march 1984