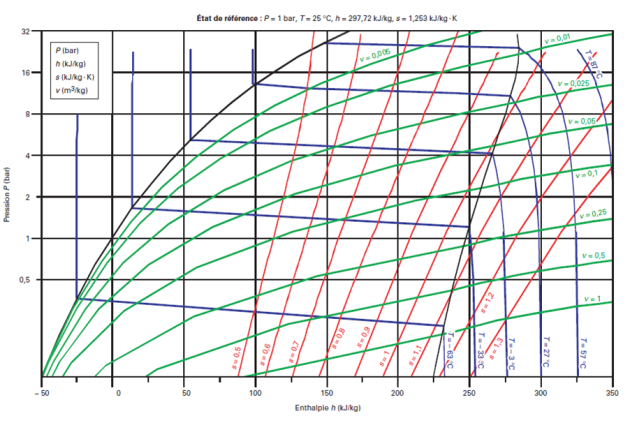
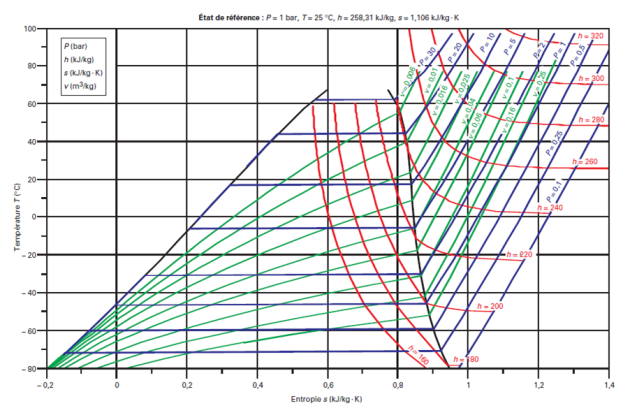
Méthodologie du calcul des propriétés thermodynamiques et des équilibres de phase des mélanges
Les progiciels génériques pour le calcul des équilibres de phase[1] des corps purs et des mélanges ont pour finalité le calcul des propriétés de mélanges mettant en jeu de nombreux fluides, avec des compositions très variables selon les cas. Il s'agit d'un problème scientifique très complexe qui mobilise de nombreux chercheurs de très haut niveau depuis des décennies. Les connaissances fondamentales sur le sujet progressent, des bases de données de plus en plus complètes sont publiées, et des progiciels mis au point. Il n'est pas possible d'entrer ici dans le détail des options existantes.
Les différentes équations d'état envisageables sont discutées dans cette page.
Nous nous contenterons de mettre l'accent sur trois points essentiels :
les phénomènes physiques mis en jeu et les lentilles d'équilibre isobares et isothermes
les règles de mélange
la validation expérimentale des modèles retenus.
Phénomènes physiques mis en jeu
Le comportement des mélanges en équilibre liquide-vapeur est généralement différent de celui des corps purs, la fraction molaire ou massique de chaque constituant évoluant entre des limites qui dépendent de la pression et de la température, du fait de la distillation qui prend alors place. De par la présence de plusieurs constituants, le changement de phase est plus complexe que pour un corps pur. Sa représentation graphique dans un diagramme n'est simple que si le mélange est binaire, cas auquel nous nous limiterons dans cette introduction.
Pour bien comprendre les phénomènes qui se manifestent, étudions le comportement d'un mélange binaire de propane et de butane. Quelques-unes des propriétés de ces corps purs (pression et température critiques, températures d'ébullition à 1 et 2 bar) sont indiquées dans le tableau ci-dessous. Elles montrent que le propane est beaucoup plus volatil que le butane, puisque à 1 bar, ils s'évaporent respectivement à - 42,4 °C et 0,7 °C.
Pc (bar) | Tc (°C) | Tsat (1 bar) (°C) | Tsat (2 bar)(°C) | |
|---|---|---|---|---|
propane | 42,48 | 96,7 | -42,4 | -25,4 |
butane | 37,98 | 152,01 | -0,7 | 18,8 |
Lentille d'équilibre isobare
Considérons un mélange de ces deux corps, et examinons comment il évolue, à pression constante, lorsque sa température change. La figure ci-dessous, appelée lentille d'équilibre isobare, montre le diagramme de phase de ce mélange à la pression de 2 bar.
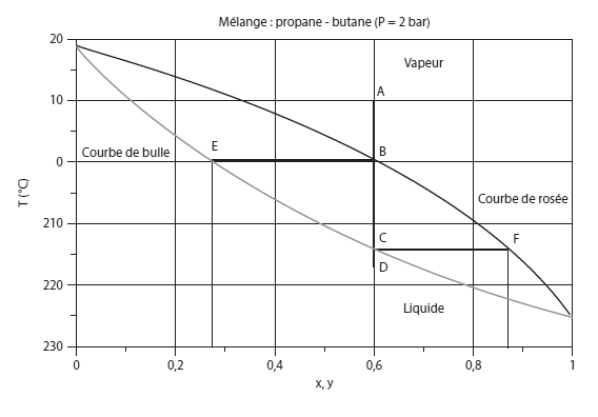
La zone vapeur correspond à la partie supérieure droite du diagramme, la zone liquide à la partie inférieure gauche, et l'équilibre liquide-vapeur à la lentille délimitée par les courbes de rosée et de bulle. L'abscisse représente la fraction molaire en propane, ce qui signifie que la valeur 0 correspond à du butane pur (Ts = 18,8 °C), et la valeur 1 à du propane pur (Ts = - 25,4 °C).
Comme c'est l'usage lors de l'étude des mélanges de vapeurs, x représente les fractions molaires en phase liquide, y les fractions molaires en phase vapeur, et z les fractions molaires globales.
L'ordonnée est la température, exprimée en °C.
Considérons un mélange de composition donnée (ici z1 = 0,6 pour le propane, z2 = 1 - z1 = 0,4 pour le butane) à l'état de vapeur, correspondant au point A de température 10 °C. Si on refroidit le mélange à pression constante (par exemple dans un échangeur), son point caractéristique se déplace le long du segment A-B vertical tant qu'il reste à l'état de vapeur.
En B, à 0 °C environ, la distillation commence sur la courbe de rosée (ou courbe de goutte), ainsi nommée parce que la première goutte de liquide apparaît. Les deux composants se liquéfient ensemble, mais, étant donné que le butane est moins volatil que le propane, il se condense davantage, de telle sorte que la composition de la première goutte diffère de la composition moyenne z. La fraction molaire x à l'état liquide du composant 1 (ici le propane) est donnée par l'abscisse du point E sur la courbe de bulle, appelée ainsi car, dans un processus inverse d'évolution de la température, c'est sur cette courbe que les premières bulles apparaissent (ici x1 = 0,28), et la fraction molaire du butane liquide est donc x2 = 1 – x1 = 0,72.
Au fur et à mesure que le refroidissement se poursuit, la composition de la phase liquide évolue, la fraction molaire du propane étant donnée par l'abscisse de l'intersection de la courbe de bulle et de l'isotherme correspondante, son point figuratif se déplaçant de E à C, tandis que celui de la phase gazeuse passe de B à F. Au point C, il ne reste que du liquide, à l'exception d'une dernière bulle de gaz, de composition y1 = 0,85 en propane et y2 = 1 - y1 = 0,15 en butane. Au-delà, le mélange reste à l'état liquide, avec sa composition initiale.
En d'autres termes, à pression donnée, le changement d'état du mélange ne se fait pas à température constante, mais avec un glissement de température (ou intervalle de distillation) qui peut être plus ou moins important selon le mélange considéré.
Par exemple, pour le mélange précédent et la pression de 2 bar, le glissement de température est de 14 °C.
Lentille d'équilibre isotherme
Examinons maintenant une évolution du mélange à température constante et pression variable. Sur le diagramme de la figure ci-dessous, appelé lentille d'équilibre isotherme, les abscisses représentent le titre en propane et les ordonnées la pression, exprimée en bar.
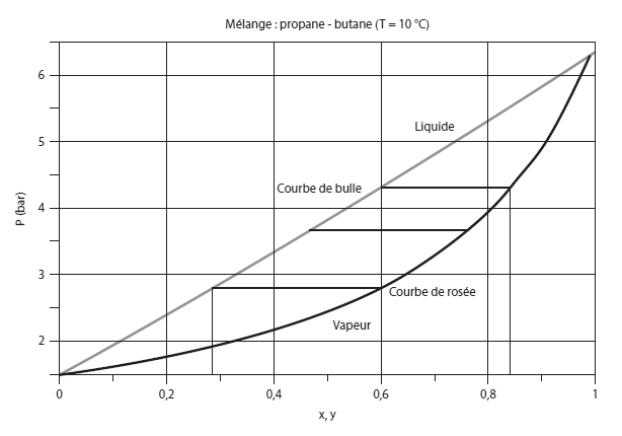
Supposons toujours que le mélange a pour composition globale (z1 = 0,6 et z2 = 0,4). Si la pression est inférieure à 2,78 bar, le mélange est entièrement à l'état de vapeur, et si elle est supérieure à 4,3 bar, il est entièrement liquide.
Entre ces deux pressions, il est en équilibre liquide-vapeur, et la composition du mélange évolue continûment dans les phases liquide et vapeur.
Pour P = 2,78 bar, la phase liquide a une composition (x1 = 0,28 ; x2 = 0,72), pour P = 3,7 bar, elle vaut (x1 = 0,48 ; x2 = 0,52), et pour P = 4,3 bar elle correspond à la composition globale.
En phase vapeur, les compositions sont les suivantes : (y1 = 0,6 ; y2 = 0,4) pour P = 2,78 bar, (y1 = 0,77 ; y2 = 0,33) pour P = 3,7 bar, et (y1 = 0,85 ; y2 = 0,15) pour P = 4,3 bar.
Mélanges azéotropes
Un cas particulier correspond aux mélanges dits azéotropes où les courbes de bulle et de rosée se rejoignent pour une composition globale donnée. On peut démontrer qu'un mélange azéotrope correspond à un extremum de pression à température constante, ou de température à pression constante. Un tel mélange se comporte en pratique comme un corps pur.
Enfin, lorsque le glissement de température est petit (< 1 °C), l'erreur que l'on commet en négligeant la distillation est très faible. On parle alors de mélange quasi-azéotrope.
C'est parce que le glissement est important, et permet de bien illustrer les phénomènes particuliers aux mélanges, que nous avons choisi ici le mélange propane / butane.
Diagrammes des fluides frigorigènes à glissement de température
Deux préoccupations environnementales sont venues remettre en cause l'utilisation massive des anciens fluides frigorigènes : la rupture de la couche d'ozone et l'augmentation de l'effet de serre. Très rapidement a été prise la décision d'arrêter la production des chlorofluorocarbones CFC) et des halons, et de remettre en cause celle des hydrochlorofluorocarbones (HCFC), du fait qu'ils contiennent toujours du chlore. L'ensemble de ces mesures a provoqué pour les industriels de la réfrigération une révolution technologique majeure qui a commencé en 1994 et qui n'est pas terminée.
Les fabricants de fluides frigorigènes considèrent en effet qu'à l'exception du R134a, il est maintenant peu probable de trouver des fluides purs qui possèdent des propriétés thermodynamiques leur permettant d'être de parfaits substituts aux anciens fluides. En revanche, en mélangeant des fluides purs dans des proportions bien choisies, il est possible d'obtenir des caractéristiques mieux adaptées, ce qui explique l'intérêt que suscitent les mélanges.
Le comportement des mélanges en équilibre liquide-vapeur est cependant généralement différent de celui des corps purs, le titre de chacun des constituants évoluant entre des limites qui dépendent de la pression et de la température, du fait de la distillation qui prend alors place.
Pour les applications frigorifiques, la composition d'un mélange frigorigène reste invariable dans les phases vapeur et liquide (si l'on néglige l'influence de l'huile de lubrification).
Dans la zone d'équilibre liquide-vapeur, ce n'est plus strictement vrai, mais on peut cependant presque toujours se dispenser de calculer avec précision la composition exacte de la phase gazeuse et de la phase liquide en sortie de détendeur et dans l'évaporateur.
Par analogie avec les corps purs, on généralise la notion de titre en vapeur par celle de titre moyen, égal à la masse de la phase vapeur, tous constituants confondus, rapportée à la masse totale des phases liquide et vapeur.
On peut alors se contenter d'un modèle du mélange à composition fixée, beaucoup plus simple. Une équation numériquement ajustée sur les valeurs expérimentales d'un mélange donné sera ainsi à la fois beaucoup plus précise et plus facile à calculer que la formulation générale que nous venons de voir. Par ailleurs, des équations d'état ont été spécifiquement développées pour ces applications.
Essentiellement, à pression donnée, les différences entre les températures saturantes des constituants introduisent comme nous l'avons vu un glissement de température dans la zone d'équilibre liquide-vapeur : la température de début d'ébullition (température de bulle) est inférieure à la température de fin d'ébullition (température de rosée), alors qu'elles sont égales pour les corps purs.
De ce fait, la pression et la température ne restent plus constantes lors d'une ébullition ou d'une condensation.
Dans les diagrammes de Clapeyron (P, v), entropique (T, s), et (h, ln(P)), les isobares ou les isothermes ne sont plus simultanément horizontales dans la zone d'équilibre liquide-vapeur comme le montrent les figures ci-dessous.
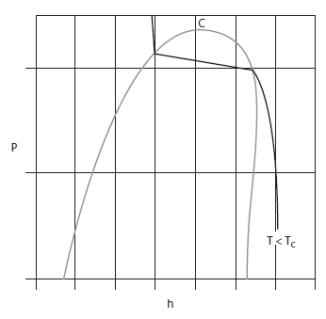
Voici le diagramme (h, ln (P)) du R404A.
On distingue nettement le glissement de température.
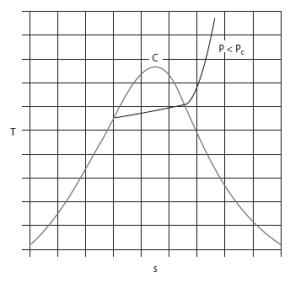
Voici le diagramme entropique (T, s) du R404A.
La variation de pression à température donnée dans la zone d'équilibre liquide-vapeur y est moins nettement perceptible.
Les deux diagrammes ci-dessous montrent l'allure d'un cycle de réfrigération au R407c dans le diagramme (h, ln(P)) et le diagramme entropique.
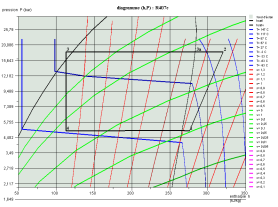
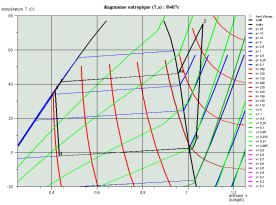
Calcul des mélanges de fluides idéaux, loi de Dalton
Beaucoup de fluides thermodynamiques en phase vapeur peuvent être assimilés à des gaz idéaux, dans un large domaine de températures et de pressions. Il faut notamment que la combinaison température-pression s'écarte suffisamment de la zone de condensation possible (c'est-à-dire que la pression ne soit pas "trop" élevée, ni la température "trop" basse). De telles conditions sont couramment réalisées pour des gaz dits "permanents" tels que, à pression et température ambiantes, l'hydrogène, l'oxygène, l'azote, le mélange oxygène-azote qui constitue l'air sec... Même la vapeur d'eau dans l'atmosphère se comporte pratiquement comme un gaz idéal tant que sa pression partielle reste modérée.
Le modèle de gaz idéal est basé sur l'hypothèse que les interactions moléculaires du gaz peuvent être négligées, à l'exception des collisions entre elles. La théorie cinétique des gaz permet alors d'expliquer le comportement macroscopique du gaz à partir de considérations mécaniques et statistiques sur les mouvements de ses molécules.
L'hypothèse fondamentale des gaz idéaux est que leur énergie interne (ainsi que leur enthalpie) est indépendante de la pression. Étant donné que tous les gaz réels sont liquéfiables, il n'existe pas de gaz rigoureusement idéal ou parfait. Ces notions sont cependant fondamentales, car la détermination pratique de l'état d'un fluide réel se fait toujours par référence au gaz idéal ou parfait correspondant, dont son comportement se rapproche à très basse pression et /ou très haute température.
La loi de Dalton postule que la pression, l'énergie interne, l'enthalpie et l'entropie d'un mélange de gaz idéaux à la température T et à la pression P sont respectivement la somme des pressions, des énergies internes, des enthalpies et des entropies partielles des gaz constituants, c'est-à-dire pris séparément à la température T et à leur pressions partielles.
Physiquement, cela signifie que les champs de forces moléculaires des différents constituants n'interfèrent pas entre eux.
La loi de Dalton signifie qu'un mélange de gaz idéaux se comporte lui-même comme un gaz idéal. Elle a pour conséquence que les résultats établis pour les gaz idéaux peuvent être utilisés pour calculer les évolutions des mélanges de ces gaz, ce qui est d'une importance capitale en pratique.
Calcul des mélanges de fluides réels, règles de mélange
Malheureusement, la loi de Dalton n'est plus valable pour les fluides réels, pour lesquels l'augmentation de la pression et/ou l'abaissement de la température conduit à invalider le modèle des gaz idéaux. C'est notamment le cas à proximité de la zone d'équilibre liquide-vapeur : lorsqu'un fluide ne satisfait plus à l'équation des gaz idéaux, son énergie interne et son enthalpie ne sont plus fonction uniquement de la température.
Lorsque l'on cherche à représenter les propriétés d'un mélange de fluides, il faut commencer par choisir une équation d'état appropriée pour les différents fluides, puis se donner des règles de mélange permettant de calculer les coefficients de l'équation du mélange à partir de ceux des corps purs.
Dans le cas où l'équation d'état choisie est une cubique, les règles de mélange les plus employées concernent le calcul des coefficients a et b. Pour a, la règle de mélange quadratique communément employée est donnée par l'équation ci-dessous.
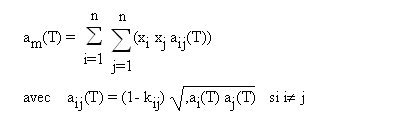
Les coefficients kij doivent être soit déterminés expérimentalement, soit estimés. On fait généralement l'hypothèse que les coefficients d’interaction binaire peuvent être utilisés même pour des mélanges d'ordre supérieur à trois, supposant ainsi implicitement que les interactions ternaires et d'ordre plus élevé sont négligeables.
Validation expérimentale des modèles
Il importe de savoir qu'une erreur dans la détermination des coefficients d'interaction peut conduire à des résultats tout à fait faux. Considérons à titre d'exemple le mélange eau/ammoniac utilisé dans les machines de réfrigération à absorption.
En utilisant l'équation de Peng Robinson pour ces deux fluides (malgré l'imprécision mise en évidence précédemment pour l'eau), il est possible de modéliser le mélange avec un progiciel tel que PE 2000, qui introduit aussi des coefficients d'interaction lij pour le coefficient b.
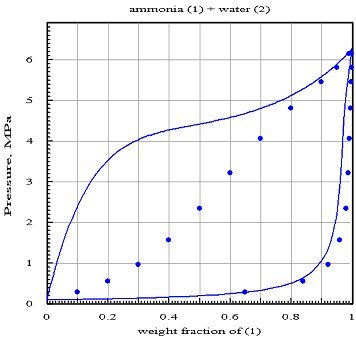
La figure ci-dessous présente d'une part des valeurs de référence représentées par les points, et d'autre part la lentille isotherme à 373 K calculée en supposant les coefficients d'interaction nuls (hypothèse du mélange idéal) : la courbe de rosée semble à peu près bien représentée pour le constituant 1, mais celle du constituant 2 serait erronée, tandis que la courbe de bulle est complètement fausse.
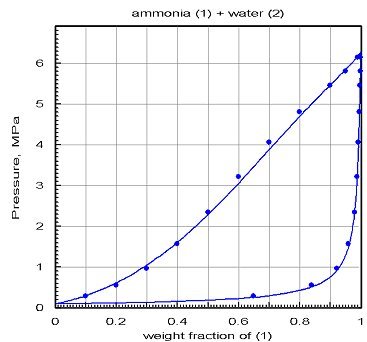
Le diagramme ci-dessous montre les résultats obtenus après optimisation par PE 2000 du calage des coefficients d'interaction : l'accord est bien meilleur.
Cet exemple montre combien il est fondamental de recourir à une validation des modèles sur la base de valeurs de référence, obtenues si possible expérimentalement, et sinon par comparaison avec des logiciels dûment validés. Le grand danger qu'il y a à bâtir des modèles de fluide à partir d'équations d'état[2] et de règles de mélange est que l'on obtient presque toujours des résultats. En l'absence de valeurs de référence, on peut être tenté de leur faire trop confiance… Il est dans ce cas recommandé d'essayer de construire différents modèles basés sur des données d'origines différentes, et de comparer leurs résultats pour lever le doute.