Modélisation des fluides associatifs
Introduction
Dans cette page, nous introduisons des équations d'état récemment proposées pour dépasser les limites rencontrées par les cubiques. Elles sont basées sur des développements de thermodynamique statistique des fluides. Parmi celles qui connaissent aujourd'hui un grand succès, notamment pour les fluides dits associatifs contenant des liaisons hydrogène, comme l'eau, du méthanol et des hydrocarbures, citons le modèle Cubic Plus Association (CPA), qui ajoute des termes complémentaires à l'équation d'une cubique, et la famille de modèles Statistical Associating Fluid Theory (SAFT).
L'équation CPA ajoute à une cubique du type Soave Redlich Kwong (SRK) ou Peng Robinson (PR) un terme associatif, tout en conservant les caractéristiques de la cubique pour les molécules non-associatives, ce qui améliore significativement leur capacité prédictive.
La théorie SAFT a été développée à partir de 1989 sur la base des travaux de Chapman, qui a proposé une théorie statistique permettant la caractérisation thermodynamique d'un fluide en incorporant les effets d'association et les différentes interactions ayant lieu entre les molécules le formant. Elle permet d'obtenir d'excellents résultats pour la modélisation du comportement des fluides associatifs, ainsi que des chaînes non-associatives.
Le principal avantage de la théorie SAFT est qu'elle repose sur une représentation physique plus réaliste des molécules en prenant en compte leur forme, leur taille, ainsi que les différentes interactions qui peuvent exister entre les molécules d'un fluide. De plus, contrairement aux équations d'état cubiques, l'équation SAFT peut représenter des molécules non sphériques ainsi que différents types de fluides (Solution d'électrolytes, solvants polaires, fluides à liaison hydrogène).
La signification physique des paramètres des équations SAFT rend possible l'élaboration d'une méthode de contribution de groupe pour leur détermination. Une version plus simple que d'autres est l'équation PC-SAFT (Perturbed-Chain Statistical Associating Fluid Theory), développée par Gross et Sadowski, considérée comme fiable dans le domaine de la modélisation des composés oxygénés et associatifs.
Modèles de thermodynamique statistique
Ces modèles étant basés sur la mécanique statistique, quelques rappels peuvent être utiles pour bien en comprendre les fondements. A partir d'une description microscopique des phénomènes, la théorie cinétique des gaz permet d'en retrouver les propriétés macroscopiques (volume, enthalpie, entropie, propriétés de transport) .
Le modèle le plus simple est celui où l'on fait l'hypothèse que la taille des molécules et les interactions entre elles sont négligeables. Il conduit à la loi des gaz parfaits.
PV = RT
La théorie des gaz parfaits est basée sur l'hypothèse que les molécules du gaz se comportent comme des sphères dures de taille négligeable, c'est-à-dire indéformables, qui entrent en collision les unes les autres et rebondissent de manière élastique, sans qu'aucune interaction n'existe entre elles.
Dans un gaz parfait, on considère ainsi que les molécules n'ont pas de volume propre et possèdent seulement une énergie cinétique du fait de leur vitesse de déplacement. Ce modèle s'applique essentiellement aux gaz sous faible pression, loin de leur courbe de saturation.
Un des grands intérêts du modèle des gaz parfaits, outre la simplicité de sa résolution, est qu'un mélange de gaz idéaux se comporte lui-même comme un gaz parfait, comme le stipule la loi de Dalton.
Précisons qu'un gaz idéal est un gaz parfait dont la chaleur massique Cp (ou encore la capacité thermique massique) varie en fonction de la température. Il suit aussi la loi PV = RT.
A la différence des gaz idéaux, les molécules des fluides réels interagissent les unes avec les autres par le biais d'interactions spécifiques. Une molécule mise en présence d'une deuxième molécule se trouve soumise à des interactions attractives et répulsives, dont l'intensité dépend de la distance entre les centres intermoléculaires, de l'orientation des molécules, et de leur structure atomique.
En tenant compte de la taille des molécules, on peut décrire les collisions entre elles, et obtenir les propriétés de transport (viscosité, conductibilité thermique, etc.).
Les forces d'attraction sont divisées en deux types : physiques et chimiques. Ce sont ces dernières qui assurent la cohésion de la molécule.
Les forces physiques sont quant à elles de nature électrostatique et se manifestent sur de longues distances. Les forces de London (dispersion) sont proportionnelles à la valeur de la polarisabilité et des potentiels d'ionisation de la molécule. Les molécules polaires possèdent un dipôle électrique qui introduit des interactions additionnelles, telles que les forces de Keesom (dipôle-dipôle), et les forces de Debye (dipôle-dipôle induit).
Les forces de van der Waals ou forces intermoléculaires correspondent à des interactions entre molécules à courte distance (entre 3Å et 8Å). Elles ne modifient pas la nature des molécules mais produisent, en moyenne, une force totale d'attraction responsable de la cohésion de la matière dans les milieux condensés.
A très courte distance (inférieure à 3Å), ces interactions deviennent répulsives et elles empêchent les molécules de se rapprocher complètement. Les forces attractives et répulsives s'équilibrent pour une distance moyenne appelée rayon de van der Waals.
En tenant compte des forces d'interaction entre les molécules, l'équation de van der Waals ci-dessous permet de décrire la transition liquide-gaz (ébullition, évaporation, condensation), mais avec une précision limitée.
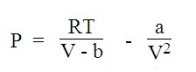
L'équation de van der Waals comporte deux termes, l'un attractif et l'autre répulsif, basé sur le modèle des sphères dures :
a, paramètre d'attraction est une mesure de l'intensité d'attraction entre molécules ;
b, appelé covolume, représente la part du volume molaire qui n'est pas réellement disponible à cause de la présence d'autres molécules.
Les équations de type Soave-Redlich-Kwong (1972) ou Peng-Robinson (1976) sont des cubiques plus précises que la précédente, très utilisées en thermodynamique appliquée. Elles considèrent que les molécules sont sphériques ou faiblement asphériques.
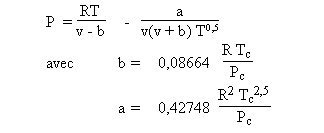
Ces équations d'état ne sont toutefois applicables que pour des molécules supposées sphériques et ne s'associant pas entre elles. Elles trouvent donc leur limite lorsqu'on les utilise pour représenter un fluide dont les molécules sont fortement non sphériques ou qui peuvent s'associer.
En introduisant des notions complémentaires présentées ci-dessous, de nouvelles théories dérivées de la mécanique statistique ont permis de mettre au point des équations basées sur le comportement moléculaire des fluides, capables de dépasser certaines limites des cubiques.
Pour bien comprendre ces nouvelles équations, il faut commencer par préciser le sens de certains concepts :
chaînes de molécules
fonctions de potentiel
liaisons hydrogène, fluides associatifs et sites d'association
Chaînes de molécules
De nombreuses molécules sont loin d'être sphériques, mais apparaissent constituées de groupes d'atomes, appelés segments sphériques, que l'on peut considérer organisés en chaînes.
Le concept de chaine de sphères dures permet de mettre au point des équations d'état comme SAFT pour représenter les polymères, ou complexes (amines, alcools, acides). La mécanique statistique permet en effet de les modéliser comme des assemblages de segments sphériques formant des chaînes.
Fonctions de potentiel
Les forces de van der Waals se traduisent par ce que l'on appelle le potentiel d'interaction intermoléculaire. Pour représenter ces potentiels plusieurs types de modèles ont été proposés, dont en particulier ceux présentés ci-dessous :
modèle de potentiel d'interaction de Lennard-Jones ;
modèle de potentiel d'interaction de fluide à puits carré.
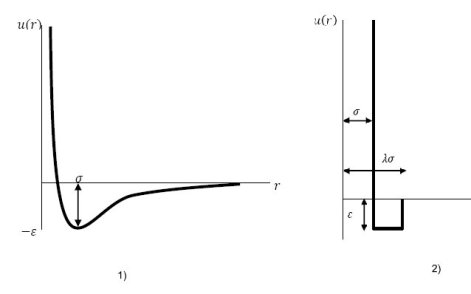
Dans les modèles thermodynamiques de mécanique statistique, les interactions entre molécules peuvent être représentées de manière simplifiée par ces fonctions de potentiel qui, utilisées avec une fonction de distribution radiale, permettent de déterminer les principales propriétés thermodynamiques des fluides, que ce soit pour les corps purs ou pour les mélanges.
Les fonctions de distribution radiale sont cependant complexes et ne peuvent être résolues facilement pour les fonctions de potentiel intermoléculaire les plus rigoureuses. En utilisant la théorie des perturbations, le problème peut être reformulé comme un développement de l'énergie libre de Helmholtz, conduisant à une forme générale non-cubique de l'équation d'état à partir de laquelle l'énergie libre peut s'exprimer. C'est ce principe qui est mis en œuvre dans les modèles SAFT et CPA.
Liaisons hydrogène et fluides associatifs
Les liaisons hydrogène sont des forces intermoléculaires existant entre un atome d'hydrogène et un atome électronégatif comme l'oxygène, l'azote ou le fluor.
La liaison hydrogène est considérée comme une force chimique ou quasi-chimique, dont l'intensité est de plusieurs ordres de grandeur supérieure à celle des forces physiques et d'un ordre de grandeur inférieure à celle des liaisons chimiques. A titre d'exemple, l'énergie d'interaction des forces de van der Waals du méthane vaut 0,6 kJ/mol, alors que celle de la liaison hydrogène de l'eau vaut 22,3 kJ/mol, et que celle d'une liaison chimique O-H vaut 465 kJ/mol.
Les liaisons hydrogène permettent la formation de polymères et de molécules complexes, à qui elles confèrent des comportements spécifiques.
A titre d'exemple, en l'absence de liaison hydrogène, la température d'ébullition de l'eau à la pression atmosphérique serait de 80 °C au lieu de 100 °C, et sa température de fusion de – 110 °C au lieu de 0 °C.
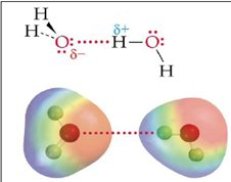
La notion de fluide associatif demande elle aussi à être bien définie. On peut qualifier les fluides associatifs comme des fluides ayant une capacité à former des liaisons hydrogène. Les molécules des fluides associatifs s'associent pour former de longues chaînes de dimères ou de polymères. Les forces intermoléculaires mises en jeu dans ces fluides sont intermédiaires entre d'une part les forces de dispersion ou les faibles interactions électrostatiques, et d'autre part les forces caractéristiques des molécules formées par réactions chimiques :
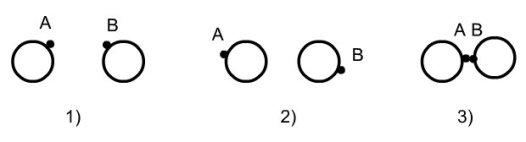
Les fluides associatifs présentent un ou plusieurs sites associatifs, chacun d'entre eux étant caractérisé par un potentiel placé proche du périmètre de la molécule. Les interactions associatives dépendent de la distance et de l'orientation des molécules. La figure ci-dessous décrit un exemple de segments sphériques munis de sites d'association A et B. Les deux sphères ne peuvent former de liaisons dimères AB que si la distance et l'orientation des sites sont favorables :
molécules trop éloignées : pas d'association ;
mauvaise orientation ;
association réalisée.
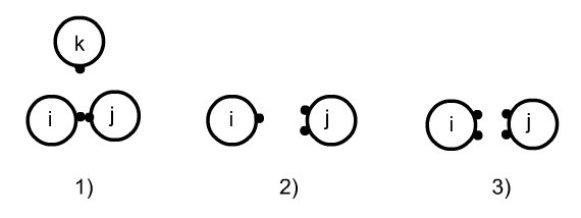
Les règles d'association sont décrites dans la figure ci-dessous :
deux sites ne peuvent pas s'associer sur un troisième ;
un site de la molécule i ne peut pas s'associer simultanément sur deux sites de j ;
la double association n'est pas autorisée.
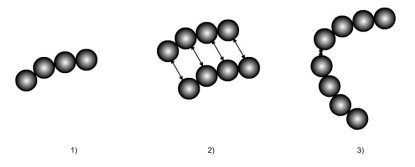
La figure ci-dessous illustre les concepts dont nous venons de parler :
une molécule complexe est modélisée comme formée de quatre segments de sphères dures ;
les forces d'interaction à distance entre deux molécules sont représentées ;
une liaison associative entre deux sites relie deux chaînes.
L'association via une fonction de potentiel à puits carré peut être caractérisée par deux valeurs, l'énergie d'association (profondeur du puits) et un paramètre caractérisant le volume d'association (lié à la largeur du puits).
L'équation CPA ajoute ainsi à une cubique un terme associatif caractérisé par deux paramètres,
 et
et
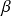 .
.
En plus de ces valeurs, il faut spécifier le schéma d'association, c'est-à-dire le nombre de sites et leur type. Ce choix demande des compétences de chimie qui sortent du cadre de cet exposé.
Le modèle nécessite donc, outre les coordonnées critiques et la masse molaire, cinq paramètres :
ceux de la cubique a, b, c, calculés ou estimés
ceux du terme associatif
 et
et
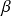 , estimés
, estimés
L'équation PC-SAFT pour fluides non associatifs est quant à elle caractérisée par trois paramètres :
m : nombre de segments
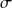 : diamètre des segments
: diamètre des segments : profondeur du puits de la fonction potentiel
: profondeur du puits de la fonction potentiel
Le modèle nécessite donc, outre les coordonnées critiques et la masse molaire, quatre paramètres :
m,
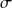 ,
,
 , estimés
, estimésw égal au facteur acentrique ou estimé
Dans les deux cas, la meilleure précision est obtenue si l'on fait un ajustement des valeurs calculées des conditions de saturation pPression, volume liquide et volume vapeur) par rapport à des valeurs expérimentales.
Il faut aussi, pour calculer les propriétés enthalpiques, se donner une loi permettant d'estimer la capacité thermique massique à pression constante Cp du gaz idéal, qui nécessite quelques paramètres supplémentaires.
En se basant sur ces concepts, les nouvelles théories dérivées de la mécanique statistique ont permis la mise au point d'équations d'état du type SAFT ou CPA permettant de représenter avec précision les propriétés thermodynamiques de fluides associatifs ou non, à molécules complexes ou polaires.
Ces nouvelles équations d'état peuvent être utilisées pour modéliser avec un petit nombre de paramètres certains fluides frigorigènes, dont les molécules sont généralement polaires mais pas nécessairement associatives.
Résultats comparatifs
Les résultats auxquels conduisent ces modèles sont illustrés par les figures ci-dessous, qui donnent le volume liquide calculé pour l'eau et le R1233zd en utilisant différentes équations d'état.
Pour l'eau, les valeurs de référence, en trait continu gras, sont celles de l'IAPWS IF-97. L'équation SRK, même avec des coefficients ajustés, ne réussit pas à fournir des valeurs acceptables : le volume calculé (en trait fin) est toujours supérieur à la valeur de référence.
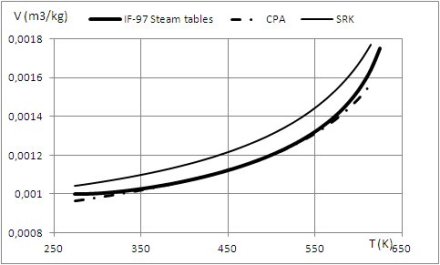
En revanche, le modèle CPA, en points et tirets fins, est excellent, grâce à la prise en compte du terme associatif, pour lequel on a considèré que la molécule d'eau comporte quatre sites associatifs, dont deux protons accepteurs d'électrons C et D (schéma dit 4C), comme indiqué dans la figure ci-dessous.
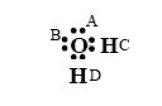
Pour le R1233zd , le modèle de référence est RefProp, en trait continu gras. L'équation de Peng Robinson (PR) en trait fin est celle qui s'en écarte le plus. Le modèle CPA (sans terme associatif), qui n'est qu'une cubique à paramètres ajustables dans ce cas, en points et tirets fins, est un peu meilleur, mais c'est le modèle PC-SAFT (sans terme associatif), qui donne les valeurs les meilleures.
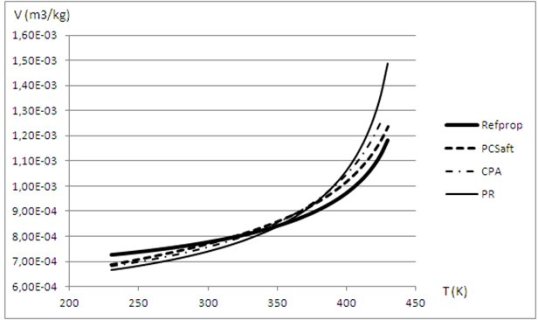
Références
Chapman W.G., Gubbins K.E., Jackson G., Radosz M., (1990), New reference equation of state for associating liquids, Ind. Eng. Chem. Res., 29, 1709-1721
Kontogeorgis G.M., Voutsas E.C., Yakoumis I.V., Tassios D.P., (1996), An equation of state for associating fluids, Ind. Eng. Chem. Res., 35, 4310-4318
Kontogeorgis G.M.,Folas G.K., Thermodynamic Models for Industrial Applications, From Classical and Advanced Mixing Rules to Association Theories, Wiley, 2010, ISBN 978-0-470-69726-9
Gross, J., Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244-1260
