Methodology for calculating the thermodynamic properties and phase equilibria of pure substances and mixtures
Methodology for calculating the thermodynamic properties and phase equilibria of pure substances and mixtures
Generic software for the calculation of phase equilibria of pure substances and mixtures are intended calculating properties of mixtures involving many fluids with varying compositions. It is a very complex scientific problem on which have been working many high-level researchers for decades. The fundamental knowledge on the subject progresses, more and more complete databases are published and software are developed. It is not possible here to go into the details of the existing options.
We will only focus on three key points:
the choice of equations of state[1];
mixing rules;
experimental validation of models.
Choice of equations of state of pure substances
When trying to determine the properties of a pure substance, one of the first challenges is the choice of an equation of state. It is known that the model of the ideal gas is characterized, in molar variables, by law: Pv = RT.
This law is only valid away from the liquid-vapor equilibrium curve for values of low pressure or high temperature. The closer we get to the saturation curve, the more the assumption that the heat capacity Cp of the substance is independent of the pressure becomes false. To determine the state of a real fluid, usually a thermodynamic chart, a table of values of the thermodynamic properties, or a set of equations of state covering the various necessary regions is used.
Many equations of state have been proposed and continue to be developed. Among the most used are the cubic equations, presented below.
Cubic equations of state
If one disregards the ideal gas model, which does not represent the real gas, the simplest models are cubic EOS, which, from a small number of variables of the fluid (molar mass, critical coordinates, acentric factor, etc.), generally provide good results in the vapor zone, but are less precise in the liquid area, especially for calculating the volume (or density).
The great advantage of the cubic EOS is that they can be formally solved, which greatly simplifies the calculation of thermodynamic properties of fluids. However, their predictive capacity is limited.
Cubic EOS are mostly derived from the equation of state originally developed by Van der Waals, which includes a term representing the forces of attraction and a term representing the repulsive interactions based on the hard sphere model.
Other cubic EOS, developed by improving each time this repulsive term, only apply to molecules assumed to be spherical and which do not associate. So they cannot be used to represent a fluid whose molecules are highly non-spherical or can associate.
One of the simplest cubic EOS is that of Redlich-Kwong which writes:
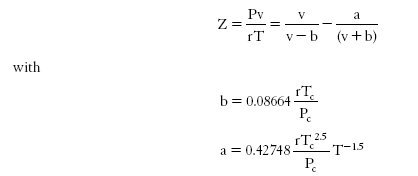
Requiring only the knowledge of the critical characteristics of the fluid, it is very general, but does not apply to all fluids with the same precision.
Various variants using an additional characteristic of the fluid, the acentric factor omega, have been proposed in the literature (Wilson, Soave, Peng Robinson...).
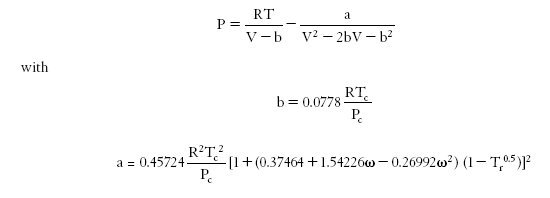
To illustrate the importance of the choice of the equation of state, we will use the PE 2000 software (PE stands for Phase Equilibria), developed by the team of Professor Brunner of the Technical University of Hamburg-Harburg. PE 2000 is a tool to correlate phase equilibrium equations with experimental data. This is a software package available freely on the Internet.
PE 2000 can determine the parameters of equations of state for pure substances on the basis of pressure and molar vapor densities in the saturation conditions. Graphics functions allow for a visual comparison of experimental and calculated data of the vapor pressure curve and PvT data.
By correlating phase equilibria related to gas extraction process, it is possible, when optimizing the parameters of equations of state for pure substances, to enforce compliance with the temperature and critical pressure of the supercritical solvent.
PE 2000 allows one to reproduce the phase behavior of binary and ternary systems, determining, for each equation of state binary interaction parameters best match for a given set of mixing rules. In addition, for a given set of interaction parameters, PE 2000 offers the possibility to calculate the phase equilibria and molar densities in all conditions.
If we have reference or experimental values, or from the literature, the PE 2000 software allows you to adjust the settings of different equations of state or interaction coefficients.
The figures below represent the chart (pressure / molar density) of ammonia, obtained with two equations of state whose parameters were optimized by PE 2000 compared with available experimental data, represented by points. In these diagrams, we showed four isotherms, corresponding to temperatures 323 K, 373 K, 423 K and 473 K.
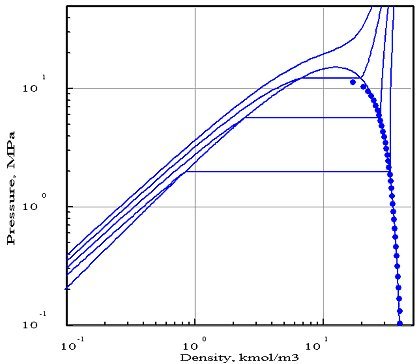
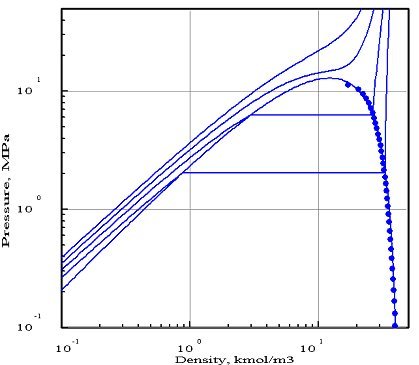
The first diagram corresponds to the Redlich - Kwong equation, and the second to the Peng- Robinson. As you can see, it gives a much better fit. In particular, the 423 K isotherm cuts the saturation curve, while the critical temperature of ammonia is equal to 405.65 K.
The Redlich - Kwong equation, which has only two parameters (in theory, the critical pressure and temperature, but the optimization compared to experimental data in this case leads to the introduction of pseudo- critical values that differ from real values), appears much less accurate than that of Peng Robinson which uses a third parameter, the acentric factor. Generally, a larger number of parameters provides better accuracy, however this is not always true.
This example shows the importance of firstly to adequately choose the equation of state, and secondly to make comparisons with the available reference data, if possible experimental.
Often, a single equation of state does not allow to obtain a good agreement with experimental data in all regions of use of the software. For example, the figure below shows the result of the optimization by PE 2000 of a Peng Robinson equation setting for water.
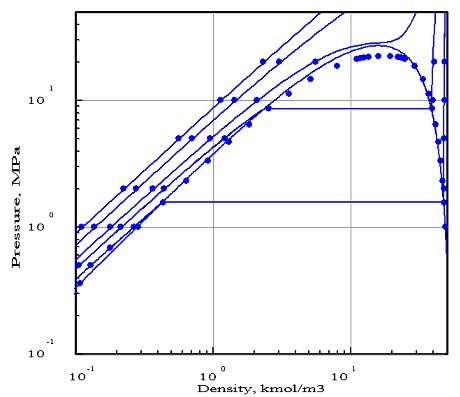
Isotherms here correspond to temperatures 373 K, 473 K, 573 K, 673 K and 873 K. The agreement with experimental data is almost good, except for the liquid-vapor equilibrium curve above 10 MPa (100 bar).
These examples have indirectly shown that cubic EOS do not always adequately represent some fluids. This is particularly true of those whose molecules are not spherical or that have hydrogen bonds. New equations of state have recently been proposed for these types of fluids, such as equation Cubic Plus Association (CPA), which adds additional terms to the equation of a cubic EOS, and the family of equations derived from Statistical Associating Fluid Theory (SAFT). A portal page is dedicated to them.
Mixtures of real fluids
This is true when the temperature - pressure combination deviates enough from the possible condensation zone (that is to say that the pressure is not " too" high, or the temperature " too" low). Such conditions are commonly valid for so-called "permanent" gases such as, at ambient temperature and pressure, hydrogen, oxygen, nitrogen, oxygen-nitrogen mixture that is dry air... Even the water vapor in the atmosphere behaves almost like an ideal gas as its partial pressure is moderate .
The ideal gas model is based on the assumption that the molecular interactions of the gas can be neglected, with the exception of collisions therebetween. The kinetic theory of gases then can explain the macroscopic behavior of the gas from mechanical and statistical considerations on the movements of its molecules.
The fundamental assumption of ideal gases is that their internal energy (and their enthalpy) is independent of pressure. Since all real gases can be liquefied, there is no ideal or perfect gas rigorously. These concepts are fundamental, however, because the practical determination of the state of a real fluid is always made with reference to the matching ideal or perfect gas, whose behavior is similar at very low pressure and / or high temperature.
Dalton's law for ideal gas mixtures
Dalton's law assumes that the pressure, internal energy, enthalpy and entropy of a mixture of ideal gases at temperature T and pressure P are respectively the sum of the pressure, internal energy, enthalpy and partial entropies of gas components, that is to say considered separately at temperature T and their partial pressures.
Physically, this means that the fields of molecular forces of the various components do not interfere with each other.
Dalton's law means that a mixture of ideal gases behaves itself as an ideal gas. It means that the results established for ideal gases can be used to calculate changes in mixtures of these gases, which is of paramount importance in practice.
Mixing rules
Unfortunately , Dalton's law is no longer valid for the real fluids for which the pressure increase and/or the lowering of the temperature leads to invalidate the model ideal gases. This is especially true near the liquid-vapor equilibrium zone: when the fluid no longer satisfies the equation of ideal gas, the internal energy and enthalpy are no longer based solely on temperature.
When seeking to represent the properties of a fluid mixture, we must begin by choosing an appropriate equation of state for the different fluids and select mixing rules for calculating the coefficients of the equation of the mixture from those of the pure substances.
In the case where the equation of state is chosen a cubic, the most widely used mixing rules relate the coefficients a and b. For a, the quadratic mixing rule commonly used is given by the equation below.
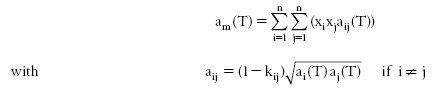
The coefficients kij must be experimentally determined or estimated. It is generally assumed that the binary interaction coefficients can be used even for mixtures of order greater than three, thus implicitly assuming that the ternary and higher order interactions are negligible.
It is important to know that an error in the determination of the coefficients of interaction can lead to quite wrong results. Consider for example the ammonia/water mixture used in absorption refrigeration machines.
Using the Peng Robinson equation for these two fluids (despite the inaccuracies highlighted above for water), it is possible to model the mixture with a package such as PE 2000, which also introduces interaction coefficients lij for the coefficient b.
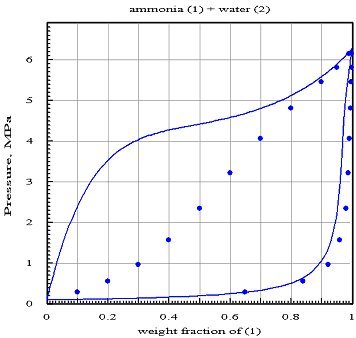
The figure below shows firstly the reference values represented by points, and secondly the isothermal lens at 373 K calculated assuming zero interaction coefficients (assumption of ideal mixture): the dew curve seems fairly well represented in component 1, but that of component 2 is erroneous, while the bubble curve is completely false.
The chart below shows the results obtained after optimization by PE 2000 of the interaction coefficients: the agreement is much better.
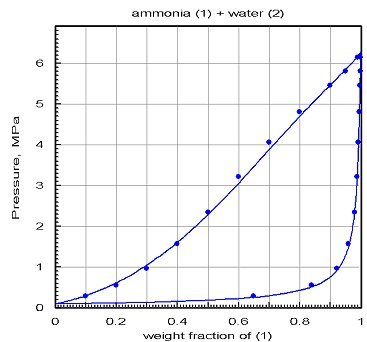
This example shows how it is essential to validate the models on the basis of reference values obtained if possible experimentally, otherwise by comparison with properly validated software. The danger of building fluid models from the equations of state and mixing rules is that one almost always gets results. In the absence of reference values, one can be tempted to trust them too much... It is recommended in this case to try and build different models based on different sources of data and compare their results to remove the doubt.
