Exergy
The theory of exergy aims to develop an integrated analysis method that includes the first two laws of thermodynamics, and thus allows us to take into account both the amount of energy put into play and its quality, which the First Law cannot do. Its interest is that it provides a quite rigorous thermodynamic framework to quantify the quality of any system, open or closed, in steady-state or not.
The first to introduce this concept was G. Gouy, who late in the nineteenth century, defined the concept of usable energy, now renamed exergy by many authors. The basic idea is to consider that a thermodynamic system interacts with what is called its environment, which behaves like an infinite reservoir at constant temperature and pressure and fixed composition, meaning that the system studied is small enough not to disturb this environment.
The environment will serve for example as a cold source for a power cycle, or hot source for a refrigeration cycle. Since the environment state determines the performance of the system studied, the theory of exergy can take it into account implicitly.
In the framework of this portal, we content ourselves with a brief and steady state (and therefore not rigorous) presentation of exergy analysis. Readers wishing to engage further in this direction will find especially in the work of L. Borel and D. Favrat (2005) a comprehensive theory of the subject.
Let us recall that Diapason session S06EN is dedicated to the exergy concept and the establishment of exergy balances, as well as a section of guidance pages .
PRESENTATION OF EXERGY FOR A MONOTHERM OPEN SYSTEM IN STEADY STATE
Let us consider a steady-state open system exchanging energy with its environment assumed to be at uniform temperature T0 (Figure below).
The energy equation is given by the First Law :
Dh + DK = t + Q
and the entropy production by the Second Law:
Q + p = T0 Ds , with 0 £ p
Ds - Q/T0 ³ 0
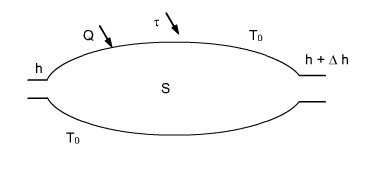
Monothermal system
If we assume that all the heat is provided by the environment, and T0 is the temperature at the boundary of the open system, Q can be eliminated by combining these two equations, giving:
t = Dh + DK - Q ³ Dh + DK - T0Ds
- t £ - (Dh + DK - T0Ds)
In most cases, we can neglect the kinetic energy changes DK.
For an open system, function xh = h - T0s is usually called exergy.
The maximum work that the system can provide is equal to the reduction of its exergy.
In practice, the actual work provided by the system may be less than this value. We define the exergy loss Dxhi, as being equal to the difference between the maximum work possible and the actual work provided:
Dxhi = (-tmax) - (-treal) = (-Dxh) - (-treal)
Dxhi = T0Ds - Dh - (-treal)
If the process is furthermore adiabatic,
(-tréel) = - Dh et Dxhi = - Dxh + Dh = T0Ds
Note that this description is not entirely satisfactory because it is clear that for a closed system, the definition of exergy leads us to consider function u - T 0 s, so that there is some ambiguity. Therefore L. Borel was moved to speak rather of co-enthalpy and co-energy.
Beyond the question of vocabulary, we note that this new function is characterized by the introduction of a variable outside the system, T0. As such, it is no longer a state function in the strict sense. However, as T0 is generally assumed to be constant, the exergy is sometimes presented as a linear combination of state functions.
Another remark can be made at this stage: exergy allows us, through the product of entropy by the environment temperature, to express variations of this state function in one dimension and by orders of magnitude similar to those usually encountered by the engineer in energy calculations, which facilitates the understanding of physical phenomena.
Finally, as discussed below, by this artifice we manage to formally eliminate from the calculations the "free" heat source represented by the environment.
Exergy can be used to evaluate the quality of the changes made in real processes, compared to ideal reversible ones.
MULTITHERMAL OPEN STEADY-STATE SYSTEM
Let us consider an open system that exchanges work and heat with n external sources at constant temperatures Tk, and environment taken at temperature T0 (Figure below).
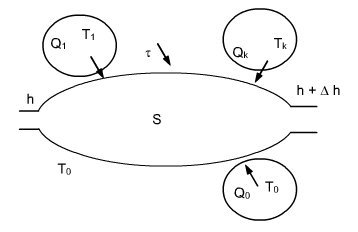
Applying the First Law gives here:
Dh + DK = t + Q0 + S Qk
and entropy production is given by the Second Law
Ds = Q0/T0+ SQk/Tk+ Dsi
Dsi, positive or zero, being the entropy generation. Neglecting kinetic energy changes, we get :
Dxh = D(h - T0 s) = t + S(1-T0/Tk)Qk - T0 Dsi (1)
or, with Dxhi = T0 Dsi >= 0:
t + S(1-T0/Tk)Qk - Dxh - Dxhi = 0 (2)
t is the work received by the system, Dxh the exergy variation of the fluid passing through it, and Dxhi the exergy dissipation resulting from irreversibilities. We call the Carnot factor the term q = 1 - T0/T. This is the factor by which we must multiply a quantity Q of heat available at temperature T to obtain the value of its exergy. If we call useful heat (or heat-exergy as per Borel) the quantity xq = q Q, equation (2) gets the form:
t + SqkQk - Dxh - Dxhi = 0
- t = Sxqk - Dxh - Dxhi (3)
The maximum engine work that can provide an open system is equal to the sum of exergy-heats of the sources with which it exchanges heat, less the change in exergy of the fluid passing through it and the exergy destroyed because of irreversibilities.
APPLICATION TO A TWO-SOURCE REVERSIBLE MACHINE
Let us consider a cyclic two-source reversible machine operating between a source at temperature T1 and environment at temperature T0. On a cycle, we have:
Applying formula (3) gives:
If T0 < T1, xq1>= 0: the system receives heat-exergy from the hot source at T1, and converts it into work t.
Here we find the Carnot cycle, whose effectiveness is
h = 1 - T0/T1.
If T0 > T1, xq1 <= 0: the system gives heat-exergy to the cold source at T1, taking it from the hot source at T0. For this, we must provide work t. It is then a refrigeration cycle or heat pump.
SPECIAL CASE: HEAT EXCHANGE WITHOUT WORK PRODUCTION
In the special case where there is no work produced, equation (3) can be rewritten as:
Dxhi = Sxqk- Dxh (4)
The exergy destroyed in the process is equal to the sum of the exergy-heats of the various sources, minus the change in exergy of the fluid passing through the system.
EXERGY EFFICIENCY
Exergy allows us to rigorously define the concept of system efficiency, and therefore to quantify its thermodynamic quality: it is the ratio of exergy uses to exergy resources. It is always between 0 and 1, and so is much greater than the irreversibilities are lower. Exergy resources is the sum of all exergies provided to the cycle from outside. Exergy uses represents the net balance of the cycle, i.e. the algebraic sum of exergy produced and consumed within it.
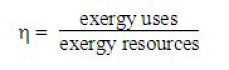
REFERENCES
A. BEJAN, G. TSATSARONIS, M. MORAN, Thermal design and optimization, Wiley publishers, 1996.
L. BOREL, D. FAVRAT, Thermodynamique et énergétique, Presses Polytechniques Romandes, Lausanne, Vol. 1 (De l'énergie à l'exergie), 2005, Vol. 2 (Exercices corrigés), 1987.
