Second Law of thermodynamics
The First Law postulates the equivalence of the different forms of energy, but it does not take into account an essential experimental fact, which is that when a system interacts with its surroundings, the energy processes it undergoes can take place only in a particular direction, that cannot be reversed without changing the system qualitatively.
Thus, heat flows naturally from one high temperature substance to a low temperature substance, but the reverse can only be achieved by using a complex thermal machine called a refrigeration machine or heat pump, or using a Peltier electrical component.
The Second Law complements the first by introducing a function called entropy, which is used to quantitatively characterize the effects of irreversibilities taking place in a system and explain the phenomena we have just discussed.
A rigorous and comprehensive presentation of the Second Law requires significant developments due on the one hand to the precautions that must be taken in writing assumptions and in explaining their connection with experience, and on the other hand to the demonstrations which must be performed.
Given the objectives of this book, it is not justified here, especially as for the calculations of applied thermodynamics we are considering here, the main practical advantages presented by this Second Law can be summarized in two points:
First entropy is as we will show the state function most closely related to heat Q exchanged with the outside (by the simple relation δQ = T ds). It therefore appears in many formal equations governing the energy components operation;
Secondly generation of entropy allows one to quantify all the irreversibilities taking place in these components and on their boundaries, which is fundamental.
That is why we selected the presentation below, sufficient for our purposes, which has the advantage of being short enough to set out and easy to understand.
Definition of entropy
At any phase are attached two quantities T and s, respectively called "thermodynamic temperature" and entropy, having the following properties:
T is a function of temperature alone, independent of the system considered
s is a function of the system state variables
in any elementary process involving heat exchange δQ with the outside δQ <= Tds, equality being satisfied if and only if the process is perfect (not irreversible).
ds = δQ/T+ dis (1)
dis, positive or zero, is called "entropy generation".
(1) can be rewritten:
δQ + δ
 = Tds (2)
= Tds (2)
δ
 is called "uncompensated work" or "uncompensated heat". It is positive for an irreversible process, and zero otherwise.
is called "uncompensated work" or "uncompensated heat". It is positive for an irreversible process, and zero otherwise.
The ex abrupto introduction of entropy can surprise and appear arbitrary. To try to explain it more gradually, we will study the case of a perfect gas, whose equation of state is written:
P v = r T
r being a constant depending on the gas (r = 287 J/kg for air), v is the specific volume, and T is temperature in Kelvin.
This equation stems from the laws of:
Gay-Lussac (in a given volume P/T = Const),
Mariotte (Pv = Const at a given temperature).
The thermal properties of perfect gases result from Joule's laws, which can be stated as follows:
First Law: the internal energy of a perfect gas depends only on its temperature.
Second Law: the heat capacity at constant volume cv is a constant.
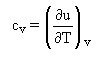
cv = du/dT
As δQ = du + Pdv, we get:
δQ = cv dT + Pdv
By replacing P by its value from the equation of state, we get:
δQ = cv dT + r T dv/v
Let ds =δQ/T = cv dT/T + r dv/v
In this form, we see immediately that 1/T is an integrating factor, and that is obviously the simplest possible. Let us recall that multiplying all the terms of a differential form dy by an integrating factor I turns it into an exact differential.
ds being an exact differential, we get:
s = cv ln(T) + r ln(v) + Cste.
The concepts of thermodynamic temperature and entropy are thus introduced naturally, entropy being the state function closest to heat. There is no evidence in this approach, however, that these concepts retain their relevance for real gases. The advantage of the axiomatic approach at the beginning of this section is that you can then retrieve the perfect gas properties as a special case of the general theory.
Irreversibility
Irreversibilities encountered in energy devices that we consider in this book, except those taking place in combustion reactions, can be grouped into two broad classes which we present succinctly:
mechanical irreversibilities due to the viscosity;
irreversibilities by temperature heterogeneity.
Mechanical irreversibility
The First Law of thermodynamics allows us to solve this problem, however, as we shall see now.
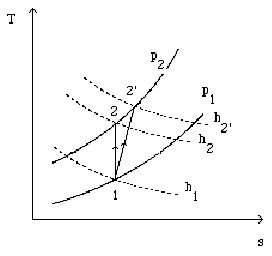
Consider an open system in which takes place an irreversible adiabatic compression, from state 1 to state 2', and such as the variations of kinetic energy can be neglected (Figure above). Given the First Law, as Q = 0, we have:
 = h2' - h1
= h2' - h1
h being a state function, it is reasonable to decompose the change in enthalpy of the irreversible compression as the succession of the two changes corresponding to the following processes:
isentropic compression from 1 to 2 involving work
fictitious isobaric heating from 2 to 2' of value
 corresponding to irreversibilities
corresponding to irreversibilities
h2' - h1= h2' – h2+ h2 – h1 =
 +
+

In conclusion
 = δ
= δ
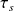 +
+
 (3)
(3)
δ
 = vdP + δ
= vdP + δ
 (4)
(4)
The reasoning can be transposed easily to irreversible expansion, as well as for closed systems, for which we have:
W = Ws +
 (5)
(5)
δW = - Pdv + δ
 (6)
(6)
These relations can be generalized to the case where the kinetic energy or mass forces must be taken into account:
δ
 + δQ= dh + dK
+ δQ= dh + dK
δ
 = dh + dK - δQ
= dh + dK - δQ
δ
 = dh + dK – (dh – vdP) = vdP + dK
= dh + dK – (dh – vdP) = vdP + dK
If the kinetic energies are not negligible: δ
 = vdP + dK
= vdP + dK
If the mass forces are not negligible: δ
 = vdP + dK + gdz
= vdP + dK + gdz
In the presence of irreversibilities: δ
 = vdP + dK + gdz + δ
= vdP + dK + gdz + δ
 (7)
(7)
These internal irreversibilities result in an increase of entropy, which can be calculated by applying the Second Law.
Irreversibility by temperature heterogeneity
The second major source of irreversibilities encountered in energy systems considered here comes from the temperature difference that must exist in practice between two bodies when they exchange heat. Indeed, for both technical and economic reasons, the exchange surfaces between these bodies are necessarily finite. It is then possible to show that the heat exchange is accompanied by an increase in entropy at the boundary between the two bodies (at temperatures T1 and T2), given by the following equation:
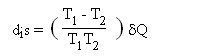
δQ being the heat absorbed by body 2. These irreversibilities are often described as external, because they take place at the boundary of the system considered.
