Basic concepts and qualitative approach of thermodynamic laws
Introduction
This page is primarily intended for users of the portal who are not professionals in the field of thermodynamics but need to acquire a minimum culture of the discipline to study thermal machines.
Many have already "done a bit of thermodynamics" but more often long ago or in some abstract way, without knowing how to put it in practice, and they generally have neither the need nor the time to invest enough in the discipline to master all the difficulties.
For various reasons, often professional, they seek to understand how operate certain energy technologies or thermal machines converting the different forms of energy and allowing for example to produce either mechanical energy from heat or cooling to from mechanical energy.
The purpose of this page is to facilitate their work by presenting as simply as possible the basic concepts they will need to use.
We start with some reminders on heat engines and the so-called thermodynamic cycles that they implement, then we define the concept of temperature, prior to distinguishing the two main modes of energy exchange taking place in these machines. We then introduce the First Law of thermodynamics, and show its implications for the main changes undergone by the fluid in thermal machines.
We then analyze the limits of the First Law and introduce the notion of irreversibility, before returning to the heat transfer and present the Second Law.
Finally, we will provide links to resources on the portal related to fluid properties.
The mind map below, prepared by A. Lambotte, summarizes most of the basic concepts that will be addressed here.
Architecture of thermal machines
The thermal machines (engines, refrigeration equipment...) are in most cases formed by assembling a small number of components providing basic functions such as heat transfer, compressions or expansions... It is for this reason that we can call them energy systems.
These components are traversed by fluids that are most often in gaseous or liquid state.
Energy technologies are therefore assemblies of components through which flow thermodynamic working fluids which undergo changes of varying complexity. In some cases, such as in reciprocating diesel or gasoline engines, the same organ (cylinder and piston assembly) is brought successively to play the role of the compressor, combustor and expansion device.
The analysis of the thermal machines is based on that of their components, which may be made done by studying the energy exchanges that take place, as we shall see in the next section. Before addressing this question, however, it is necessary to introduce a new concept which plays a fundamental role in thermodynamics, the open or closed system.
We just used the same term, system, under two different meanings, whose distinction it is important to understand. It is an inescapable problem which arises because:
common usage has consecrated the word of system to describe a set of elements interacting with each other;
while in thermodynamics, a system means a quantity of matter isolated from its environment by a fictitious or real boundary.
Specifically, a thermodynamic system is said to be closed if it does not exchange matter with the surroundings through its boundary, otherwise it is said to be open.
Beginners are often confused by the distinction between closed systems and open systems, the latter corresponding to a new concept for them because during their undergraduate tuition, they generally considered only closed systems (to avoid taking account the exchange of matter at the boundary).
In a diesel or gasoline engine, the valves are closed during compression, combustion and expansion, insulation from outside the mass of gas that is located between the piston, the jacket and the cylinder head. The processes that take place inside the engine must be calculated in a closed system. In the case of a gas turbine , compressor, combustor and turbine are crossed by a continuous flow of gas. At the entrance and exit of each of these components, matterl is transferred. The changes must then be calculated in an open system.
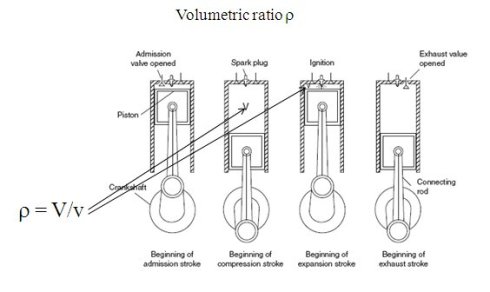
The case of reciprocating internal combustion engines is shown in the figure above, for a four-stroke gasoline engine, whose two main geometric characteristics are the displacement V and the compression ratio ro.
As the figure shows, during the intake and exhaust phases, matter enters or leaves the set (cylinder head, cylinder, piston), so that this set should be modeled as an open system. However, during the phases of compression and combustion-expansion, the valves are closed and this set should be considered as a closed system.
As the pressure varies considerably during the process, it is even better, if we want to better represent the reality, to break down the combustion in several stages: for example, first at constant volume, then constant pressure and finally at constant temperature.
There is a certain paradox in the fact that the calculations are generally easier to make for open systems than for closed systems, although they do not involve exchange of matter with the outside. The reason is that the pressure is generally known in the open system calculations while it depends on many factors in a closed system.
For example, combustion in a gas turbine (open system) takes place at constant pressure, if we neglect small pressure drops.
To complete complicate matters, it is natural (but fatal) to confuse the concepts of open and closed systems in the thermodynamic sense we have just introduced and in the sense of the complete cycle traversed by the heat engine fluid.
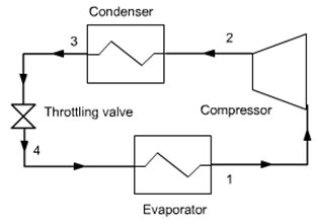
For example a compression refrigeration machine cycle is generally closed (figure below), otherwise the refrigerant would be lost to the atmosphere, which would be both costly and harmful to the environment, while each of its individual components (except possibly if the compressor is displacement ) is an open system, crossed by a steady flow of refrigerant.
The machine operates globally in a closed cycle involving several components, each working in an open system.
We have several times mentioned above the notion of cycle, which should be specified. In many practical applications, as in the example just shown, the fluid undergoes a series of processes that lead it to end up in its initial state, which justifies that we speak of the cycle.
In some cases (internal combustion engines) exhaust gases are released into the atmosphere, so it is inappropriate to speak of a cycle. However, in a simplified approach to these processes, we can assume that the thermodynamic properties of the discharging fluid are the same as those of the incoming fluid, so that we can consider that the fluid flows through a partial cycle, the said open-cycle, which could be closed by a complementary dummy process, which then allows one to compare it to other closed cycles. By extension, we are used to talking of a cycle to describe the representation of the succession of changes undergone by thermodynamic fluids being involved in energy technologies.
We are used to distinguish two main types of cycles:
motor cycles can produce mechanical energy from heat;
refrigeration cycles in which mechanical energy is used to raise the level of thermal heat or produce cooling.
In almost all engines, the fluid is always successively compressed, heated, expanded. If the cycle is open, the fluid is then discharged in the external environment. If it is closed, it is cooled and then compressed again. In all refrigeration cycles, it is compressed, cooled, expanded and heated. In the refrigeration machine that we have presented above, the fluid heating is provided through the evaporator, by cooling the cold chamber.
Concept of temperature
The concept of temperature can be introduced in several different ways. We content ourselves here with the operational definition which is based on two propositions:
we know how to construct a thermometer device, of which all physical properties are, under well defined operating conditions, function of a single variable called temperature;
we know how to get a physical system such that when a thermometer is immersed in it, its indication remains constant over time and independent of its orientation and its place.
It is said the temperature of the medium is equal to that of the thermometer and that the medium is in thermal equilibrium.
It is possible to link this presentation with the axiomatic definitions of the temperature deduced for example from the Second Law. A rigorous and comprehensive presentation of this notion, however, is beyond the limits we have set for this book. Furthermore this introduction is quite intuitive and its practical use does not generally pose a particular problem.
Another common way to introduce the temperature is based on statistical thermodynamics, which establishes that the temperature of a gas is the macroscopic magnitude representative of the state of thermal agitation of its molecules. We know that they move randomly in the gas, generating what is called Brownian motion.
Because of this movement, the molecules have a microscopic kinetic energy associated with the temperature, which explains that it depends on their velocity and thus their thermal motion.
Note that the temperature can be defined in several ways, depending on the selected zero and scale. Usually, it is expressed in degrees Celsius (°C), the zero corresponds to the triple point of water. A temperature t (°C) is equal to T-273.15, where T is the absolute temperature expressed in Kelvin (K).
In thermodynamic calculations, unless otherwise stated, T is the absolute temperature expressed in Kelvin.
Warning: you must be very careful not to confuse heat and temperature, which are two very different concepts, the latter representing an amount of energy, as discussed below.
Energy exchange between a thermodynamic system and its surroundings, enthalpy
Over the processes that they undergo in thermalmachines, fluids exchange energy with the outside or between themselves in two forms: mechanical, traditionally denoted W, and thermal, denoted Q.
There are of course other forms of energy, like electricity or the energy used in a chemical reaction, but they only intervene in specific cases.
WORK OF PRESSURE FORCES
Consider a closed system phase. External forces acting on it are usually limited on the one hand in the action of gravity on the fluid mass, and on the other hand of pressure on its boundaries.
In heat engines, the work of gravity is in most cases negligible compared to that of actions called "contact". To fix these ideas, the work provided by a mass of 1 kg of water falling from a height of 100 m is equal to 980 J, while that of the same mass of steam at 500 °C isentropically expanded from 100 bar to 1 bar is equal to 983 kJ, or 1000 times greater.
Consequently, in thermal machines, the work of mass forces will most often be negligible compared to that of pressure.
One can easily show that the work of pressure forces on a closed system of elementary volume dV is equal to dW = - P dV.
This expression, which generalizes easily to a closed system of any form, is valid only if the system remains in static equilibrium, i.e. if the following assumptions are true:
the pressure remains uniform across the system;
the fluid remains at rest.
Note that this formula implies that the work received by the system is positive, and that the work it provides is negative. By convention, we generalize this result by counting positively the energy received by a system, and negatively the energy it provides to the outside.
HEAT TRANSFER
Consider a simple fluid mass, within which no friction occurs. delta Q is the quantity of heat exchanged with the outside and received by the unit of fluid mass in an infinitely small process.
An important experimental fact, the basis of compressible fluid thermodynamics, is that delta Q is a differential form of the fluid mass state, called a calorimetric equation.
For example, in the case of a mono-variant system (equilibrium between phases during a change of state), the calorimetric equation depends only on the quality x, ratio of vapor mass to total mass (liquid + vapor) in the case of vaporization or condensation: delta Q = L dx
L is the change of state enthalpy.
For an ideal gas, depending on whether we are dealing with an open system operating at constant pressure, or a closed one operating at constant volume, delta Q = cp dT or delta Q = cv dT.
Adiabaticity
We say that a component is adiabatic when it does not exchange heat with the outside. This is a very important concept in practice, because, as we shall see, it applies to a large number of compression and expansion devices.
INTERNAL ENERGY
The distinction we have made in the previous section between open and closed systems is found when it comes to characterizing the energy contained or put into play in a given amount of matter.
It is fundamental to know that the classical notion of internal energy U can only be used for closed systems, and is not suitable for open systems because they are crossed by one or more flows of matter.
ENTHALPY
For the latter, the generalization of the internal energy is called the enthalpy H (H = U + PV). It differs from U by the product PV, sometimes called "transfer work", which is representative of the difference of state of the fluid at the component inlet and outlet.
A little later, after presenting the First Law, we will conduct a small demonstration for understanding the origin of this definition of enthalpy.
Beginners should certainly not worry about this new concept: in practice, they only need to reason considering that the enthalpy is the energy involved in a component running in an open system, and replaces in this context internal energy. Once this transposition well understood, the concept of enthalpy presents no particular difficulty.
Refer to the portal page devoted to exchanges of energy to get a more complete presentation with the associated equations.
First Law of thermodynamics
The First Law, also known as the equivalence principle or the energy conservation principle, says that the energy contained in an isolated system or evolving in a closed cycle, remains constant, whatever the processes it undergoes.
The various forms that can take the energy of a system: mechanical energy, heat energy, potential energy, kinetic energy etc. are all equivalent to each other under the First Law.
The First Law is a conservation principle similar to that of the conservation of mass of a system, or chemical species in a reaction. So this is a concept very intuitive and easy to implement.
The First Law is written in two forms depending on whether it is expressed in closed or open system. In the first case, it involves the internal energy and in the second enthalpy.
In closed system, it is given by the well-known equation below, which can also be used to define the internal energy:
Delta U + Delta K = W + Q
Refer to the portal page devoted to the First Law to be more complete presentation with the associated equations.
Industrial operations generally take place continuously, each component (turbine, pump, valve etc.) permanently receiving and evacuating matter. When, as it is often the case, their operating conditions are stabilized, possibly periodically, it is called "permanent" or "steady-state". Consider a cyclical machine operating in open system, schematized in figure below.
In the most frequent case (Figure below) we can assume that the component operates between two chambers of large dimensions, where the fluid is in equilibrium. The upstream (1) and downstream (2) states are defined by their pressure and temperature, assumed to be uniform despite the extractions and contributions due to the suction and discharge. For example, a gas turbine compressor sucks in air and discharges into the combustion chamber where the pressure is substantially uniform.
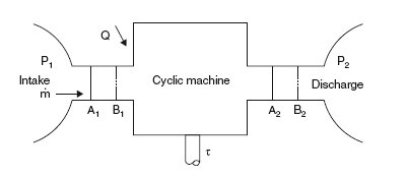
We will now establish the enthalpy form of the First Law by a simple argument, which is to follow the evolution of a closed control volume, and calculate the work of external forces on all its boundaries, distinguishing between cross sections of the fluid, fixed walls, which obviously neither produce nor receive work, and moving walls like blades, in which some work tau is exerted, called "shaft work".
In its passage from (1) to (2), each unit mass of fluid receives from the moving walls the shaft work tau, whose knowledge is fundamental, since its product by the mass flow m, gives the power involved (neglecting mechanical losses in bearings and transmission).
One can easily show that, per unit mass, a component performing any kind of processing provides work tau algebraically equal to the work of pressure forces calculated in a closed system WA, increased by the transfer work, that is to say the variation of product Pv:
The machine, traversed by a flow rate m, works in unsteady, but periodic, state that is to say all its components, including the fluid mass in it, are periodically in the same state (note that the steady-state operation is deduced from the periodic regime by letting the period tend to 0).
Consider the closed system consisting of the fluid mass contained in the initial state in the control volume limited by the fixed and movable walls and sections A1 and A2 respectively located in the entry and exit chambers.
After a period dt, the control volume has been moved and is now limited by sections B1 and B2, themselves in the entry and exit chambers. The machine has been traversed by the fluid mass m dt, common mass of sections A1B1 and A2B2 (conservation of mass flow), and has provided work on the fluid tau m dt (by definition).
The work of external forces W m dt is equal to the sum of the work of gravity and the work of pressure forces exerted on the various boundaries of the machine, four in number: A1, A2, moving walls and fixed walls.
On these, delta WA4 = 0.
On A1, a reasoning similar to that in Section 2.2.1 (the machine cannot be treated as a single phase) shows that:
delta WA1 = - P1 dV1 = - P1 (-m dt) v1 = P1 v1 m dt
On A2, in the same way, delta WA2 = - P2v2 m dt.
By definition, the shaft work is that of pressure forces on the moving walls,
tau m dt = delta WA3
We have thus:
delta W = delta WA + dWv = delta WA1 + delta WA2 + delta WA3 + delta WA4 + dWv
delta W = W dt = P1 v1 m dt - P2v2 m dt + tau m dt + dWv
tau = WA + P2v2 - P1v1 = WA + Delta (Pv)
Recall the equation for the First Law in a closed system:
Delta U + Delta K = WA + Q
By adding Delta (Pv) to its two members
Delta U + Delta (Pv) + Delta K = WA + Delta (Pv) = tau + Q
Delta H + Delta K = tau + Q
This little demonstration explains the orignin of the equation that relates the enthalpy to the internal energy. The term Delta (Pv) represents the difference between the useful work carried out at the moving walls of the machine and that of all the pressure forces on the boundaries of the latter.
This notion of shaft work is far from trivial. In practical terms however, it poses no particular problem; in all the compression and expansions in open systems, the useful shaft that must be considered in the calculations.
Evolutions of reference and applying the First Law in an open system
The enthalpy form of the First Law for a component through which a fluid is given below, the notations being those of the book Energy Systems.
C being the velocity of the fluid, the First Law applied to a component through which passes a fluid, the unit flow-rate can be expressed in mass units in the form:
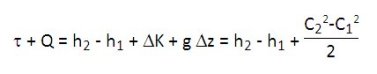
For most heat engines, the term g Delta z is negligible. In many cases, the variation of kinetic energy is low vis-à-vis other changes (except of course in special cases such as jet engines, some turbomachinery blades or expansion devices).
Under these conditions, the amount of work received or provided and the heat exchanged with the outside by the component is equal to the change in enthalpy of the fluid passing through it.
This fundamental relationship explains why, in industrial devices, it is virtually impossible to implement both great mechanical work and a significant heat flux.
For the calculation of processes, these findings are very important in practice since they indicate that in most components of industrial machinery, mechanical and thermal exchanges are decoupled. They also explain why the enthalpy is a state function widely used in open system processes: the change in enthalpy of the fluid represents the mechanical or thermal energy put in.
Heat exchange
Components which transfer heat from one fluid to another require large exchange areas, their heat fluxes being proportional to these areas. Technical and economic considerations lead to the adoption of purely static devices. For example, large bundles of tubes in parallel, traversed internally by one fluid while the other flows outside.
tau is zero because of the absence of movable walls.
In a heat exchanger, heat Q transferred or provided by one fluid to another is equal to its enthalpy change Delta h.
Combustion chambers, boilers
The same reasoning applies to the combustion chambers or boilers, which can generally be regarded as isobaric.
In a combustion chamber or boiler, heat Q transferred to the fluid passing through it is equal to its enthalpy change Delta h.
Compression and expansion with work
Expansion can be made with and without work. In the first case, the machine most commonly used is the turbine. In the second case, it is a simple valve or a filter (see below).
Machines doing the compression or expansion of a fluid have a very compact design for reasons of weight, size and cost. For similar reasons, they rotate very fast (several thousand revolutions per minute). Each parcel of fluid remains there very briefly.
Moreover, fluids brought into play in compressors and turbines are often gas whose heat exchange coefficients have low values
Short residence time, small areas of fluid-wall contact, and low exchange coefficients imply that the heat exchange is minimal and that the operation of these machines is nearly adiabatic: Q = 0.
In a compression or expansion adiabatic machine, shaft work tau is thus equal to the change in enthalpy of the fluid Delta h.
Expansion without work: valves, filters
There is a class of devices, such as the expansion valve of the refrigeration machine, where tau and Q are both zero, i.e. Delta h = 0: they are static expanders such as valves and filters. The corresponding process is called an isenthalpic throttling or a flash expansion.
Limits of the First Law
A major limitation of the First Law of thermodynamics is the failure to take into account the quality of energy: indeed different forms of energy expressed in kWh are equivalent, but the possibilities of converting one form of energy into another are not.
Thus, work can still be fully converted into heat, but the converse is not true.
The work is one form of energy whose quality is among the best, and which can therefore be taken as a reference.
We can rephrase this by saying that a possible indicator of the energy quality is its ability to be converted into work.
One can convert electricity into work using an electric motor of efficiency over 98%, or conversely convert mechanical work into electricity through a generator of equivalent efficiency, which means that these two forms of energy are about the same quality.
Notion of irreversibility
In the example of power conversion work we have just given, we stated that the machines used had excellent efficiencies, close to but slightly lower than 1: experience indeed shows that, whatever precautions are taken, some energy is degraded. The First Law teaches us that the total energy is conserved, but some of its quality declines and ultimately ends up as heat, because of friction, Joule losses etc.
These losses are called irreversibilities, because the process work --> electricity --> work is not completely reversible: part of the initial work is converted into heat.
Heat transfer, conversion of heat
In the particular case of heat, it is experimentally verified and this is always true, without exception, that the heat transfer between two media at different temperatures is always from the hottest (whose temperature is higher ) to the coldest (the one whose temperature is the lowest).
We also see that a heterogeneous system consisting of two media at different temperatures being not insulated from each other always evolves towards a homogeneous state at intermediate temperature.
Moreover, when attempting to convert heat into work, experience shows that it is first necessary to have two sources of heat, one at high temperature, and the other at low temperature.
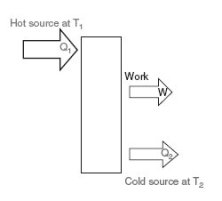
In addition, the larger the temperature difference between the sources, the greater the amount of work that can be converted from one kWh of heat.
Temperature thus also appears as a possible indicator of the quality of heat.
A further remark can be made at this stage: it is the existence of a temperature difference between two media that allows the production of work to be possible.
Concept of phase
A phase is a continuous medium having the following three properties:
it is homogeneous (which implies a uniform temperature);
speed in each point is zero in a suitable reference frame;
it is subject to no external force at distance (uniform pressure).
As is known, matter exists in three phases: solid, liquid and gas. A thermodynamic system may consist of a single pure substance, or have several. In the latter case, the mixture is characterized by its molar or mass composition. Each of the components of the mixture may be present in one or more phases. If the components and their phases are uniformly distributed throughout the volume defined by the system boundaries, the mixture is homogeneous, otherwise it is heterogeneous. The properties of a mixture depend obviously on its homogeneity.
The concept of phase plays a very important role in practice, because we always assume in what follows that any physical system is decomposed into a set of phases.
Second Law of Thermodynamics
The considerations which have been exposed gradually led to the enunciation of the Second Law of thermodynamics and the introduction of a quantity called entropy, which can be interpreted in many ways, especially as the simplest state function showing the heat exchange of a system with its environment.
His main interest in practice is to facilitate the calculations you need to perform when you want to properly take into account the quality of energy in the study of conversions between its different forms. In particular it allows to quantify precisely the irreversibilities taking place in heat engines.
The Second Law can be stated as follows: at any phase are attached two quantities T and s, respectively called "thermodynamic temperature" and entropy, having the following properties:
• T is a function of temperature alone, independent of the system considered;
• s is a function of the system state variables;
• in any elementary process involving heat exchange delta Q with the outside delta Q <= Tds, equality being satisfied if and only if the process is perfect (not irreversible).
The second principle thus states that any real transformation takes place with the creation of entropy.
It can also be expressed as follows: any transformation of a thermodynamic system is performed with increasing global entropy, including the entropy of the system and the external environment. We then say that there is creation of entropy.
The second principle is due to S. Carnot, who in 1824 demonstrated that the efficiency eta of a heat engine ideal cycle is described by eta = 1 - Tc/Th, Th and Tc being the absolute temperatures of the hot and cold sources with which the machine exchanges heat.
Carnot has shown that this efficiency does not depend on the nature of the machine nor the working fluid used, but only on Th and Tc.
Refer to the portal page devoted to the Second Law to get a more complete presentation with the associated equations.
Application of the Second Law to industrial processes
HEAT EXCHANGERS
In a heat exchanger heat can be transferred between the two fluids only if there exists between them in practice a certain temperature difference. Indeed, for both technical and economic reasons, the exchange surface between these fluids is necessarily finite. It is then possible to show that the heat exchange is associated with an increase of entropy.
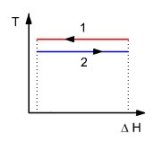
To simplify the calculations, we will consider a heat exchanger between a hot fluid 1 which condenses and a cold fluid which vaporizes 2 (figure above), which allows us to consider that the two fluids remain at the same temperatures T1 and T2.
For such an exchanger, one can show that the creation of entropy is given by the following equation, Q being the amount of heat exchanged:
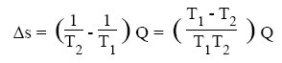
The greater the temperature difference between the fluids, the greater the creation of entropy. In a heat exchanger, there is conservation of energy (enthalpy) released by the hot fluid to the cold fluid, but the transfer being done with a drop in temperature, there is creation of entropy.
COMPRESSORS AND TURBINES
We have said above that the compression and expansion devices are generally adiabatic (δQ = 0). By definition of the Second Law, δQ = 0 <= Tds, equality being verified if and only if the process is perfect (not irreversible).
In a perfect adiabatic compressor or turbine, there is no creation of entropy. We say that the evolution is isentropic, very important concept in practice because it is the reference process against which actual processes are characterized.
Implications for the production of work from heat
The first two laws have many implications when trying to produce work from heat. We limit ourselves here to present some of them.
First, it is imperative to have two sources of heat, one at high temperature Th and the other at low temperature Tc. The hot source provides heat Qh to the heat machine, which converts part P in the form of mechanical power, and rejects Qc to the cold source.
Second, under the First Law, Qh = Qc - P. We call effectiveness or efficiency of the machine the ratio epsilon = P / Qh.
The higher Th, the higher epsilon can be, knowing, according to the Second Law, that e can not be less than the Carnot efficiency defined above, eta = 1 - Tc/Th.
In practice, epsilon is often much lower than the Carnot efficiency eta, as many irreversibilities exist in the heat engine.
Another practical implication of what we have seen is that we must seek to minimize the irreversibilities. We refer you to the portal page devoted to qualitative analyzes of cycles for more explanation on this subject.
Fluid properties
If, as we have assumed at the beginning of this page, you are not experts in thermodynamics, it is essential that you familiarize yourself with the properties of fluids that are used in thermal machines, and at least with those of the pure substances.
We suggest two possible approaches to this:
refer to the presentation page of the properties of pure substances ;
study Diapason session S04aEn (Properties of substances, usual charts) .
