The optimization of an energy system always depends primarily on the overall context in which the technology fits. It is therefore essential to first examine the context, including the regulatory framework, especially in relation with the environment, as well as the alternatives.

A second important aspect to consider is that of technological and economic constraints, particularly in terms of material durability.

These points being well in mind, the qualitative and quantitative analysis of cycles may shed particularly interesting light on the possible optimizations.

Among others, the comparison with the Carnot cycle is almost always required.

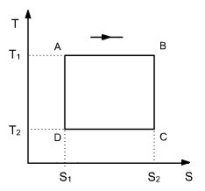
The Carnot cycle being the one that leads to the best effectiveness, it is almost always interesting to compare actual cycles to it. It concerns the shape of the cycle and the nature of the irreversibilities encountered, which are mainly of two types: mechanical and due to heterogeneities in temperature. The plot of the cycle on the usual charts makes it possible to visualize the shape and facilitates the analysis.

We know that the effectiveness of such a cycle is equal to eta = 1 - T2/T1, T1 and T2 being respectively the temperatures of hot and cold sources (Figure above).

This value is the maximum efficiency for a two-source machine, but the realization of a Carnot cycle presents many difficulties because we are generally conducted for different reasons to use fixed devices to exchange heat, and adiabatic machines to achieve compressions and expansions.

Specifically:

• In practice, there must be some difference in temperature between the machine and the hot and cold sources in processes AB and CD;

• It is unusual that hot and cold sources may be considered isothermal: in most cases it is a fluid which exchanges heat between two temperature levels;

• Achieving isothermal compression CD or isothermal expansion AB poses many technological problems;

• When the compression and expansion are adiabatic , they are not isentropic due to mechanical irreversibilities;

• Even when the compression and expansion are assumed isentropic, the temperatures reached at the outlet of these processes are not equal to those of hot or cold sources.

The actual engine cycles differ significantly from the Carnot cycle, the isotherms AB and CD being most often replaced by isobars or isovolumes. However, we seek of course the expansion BC and the compression DA to approach isentropic

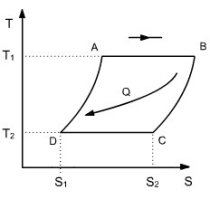
We can imagine cycles where the isentropic compression AD and expansion BC are replaced by other processes, each of them being deduced from the other by a translation in the entropy diagram (Figure above). This is called regeneration.

In these circumstances, it is theoretically possible to make all the internal and external heat exchanges at constant temperature, and the ideal cycle with regeneration reaches the same efficiency as that of the Carnot.

In practice, the internal heat exchange is of course not at constant temperature, and we introduce the notion of regenerator effectiveness to characterize performance.

What essentially distinguishes cycles, are firstly the states (gaseous or liquid) in which the working fluid is likely to be, and secondly the nature of the changes it undergoes.

The study of heat engines allows, from the theoretical thermodynamic cycle analysis, to include all the constraints that one faces when trying to convert heat into mechanical or electric power, or vice versa mechanical energy in heating or cooling.

In practice, as we shall see, many technological difficulties arise, and real cycles often deviate significantly from the theoretical cycles we can calculate. The study of a particular machine thus depends heavily on the technical devices, especially mechanical and thermal, which are involved, and we will try in what follows to take into account these peculiarities as far as possible.

The presentation of theoretical cycles still is of great interest because they represent the thermodynamic reference, and determine the limits it is possible to achieve in terms of efficiency, for example. The study of cycles can thus effectively guide the engineer in his approach to improving engines.

Qualitative analysis have the advantage of being relatively easy to make and promote the development of physical sense among those who use them, including students. To go beyond, it is necessary to perform quantitative analysis, based mainly on the establishment of exergy balances presented in another section .