We have seen that, in industrial processes, operations usually take place continuously, i.e. in open systems. It is therefore the enthalpy First Law expressions that apply most often.

Although it is known to almost everyone, experience shows that its implementation may pose some difficulties. It suffices, however, to be able to apply the conservation law of extensive energy quantities (shaft work, heat exchanged with the outside Q, enthalpy flow of the fluids involved) to an appropriate control volume, which most often is none other than the system defined by the boundaries of the component studied. Given the First Law, enthalpy is a conservative quantity, and the First Law is simplified, terms of generation and consumption disappearing, to become:

If we assume that the system operates in steady-state mode, which is usually the case, there is no net accumulation in the control volume, and this equation results in:

Consider for example the case of an adiabatic gas turbine axial compressor, sucking air at rest in the atmosphere, and discharging into the combustion chamber of the machine

The control volume in this case corresponds to the geometry of the compressor, bounded upstream and downstream by its connecting flanges.

The mass balance is very simple to set up, because, noting with index 1 the inlet in the compressor, and 2 the outlet:

m1 = m2 in steady-state

The machine being adiabatic, there is no heat exchange with the outside, and therefore Q = 0. At suction as well as at discharge, the air velocity is low and its kinetic energy negligible. The enthalpy balance of this machine is very simple:  Δh = . The enthalpy communicated to the fluid is equal to the work received on the shaft.

If the compressor is cooled, the balance is slightly more difficult. If the heat exchanged with outside is Q < 0, we have: Δh = + Q. The enthalpy communicated to the fluid is equal (in absolute value) to the difference between work received on the shaft and heat extracted.

Now let us consider a slightly more complex example, on closed systems. This is the combustion in a diesel engine, modeled as a succession of two elementary combustions (called mixed cycle): first at constant volume, then at constant pressure.

Mass balance is this time a little more complicated, mc being the mass of fuel injected during each phase of combustion: m2 = m1 + mc

The control volume is in this case the whole set: head, cylinder and piston. The engine being cooled by water, the combustion is not adiabatic.

The first combustion phase taking place at constant volume, it does not involve any work (W = 0), and energy balance should be written here 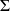ΔUi = Q, the summation being performed on all species present, assumed to be ideal gases. A first problem exists here, because this equation assumes that the calculation of the internal energy of gases present in the chamber is done taking into account the state of the combustion reaction, i.e. considering the changes in chemical variables.

However it is very rare in industrial practice that we operate as indicated previously: the internal energy (or enthalpy) of an ideal gas is generally defined in relation to the standard reference of 1 bar and 298 K for a given composition.

To overcome this difficulty, it is customary, although it is formally inconsistent with the First Law, to reintroduce, rather artificially, in the balance equations a term of power generation in the volume, which corresponds to heat Qr (> 0) released by the combustion reaction. As we indicated earlier in this chapter, this approach allows us to ignore the chemical variables, and thus significantly simplifies the formalism.

For combustion phase at constant pressure, the piston is in motion and produces a shaft work W that must also be included in the balance.

C being the velocity of the fluid, the First Law applied to a component through which passes a fluid, the unit flow-rate can be expressed in mass units in the form:

We have already indicated that, for most heat engines, the term gΔz is negligible. In many cases, the variation of kinetic energy is low vis-à-vis other changes (except of course in special cases such as jet engines, some turbomachinery blades or expansion devices).

Under these conditions, the amount of work received or provided and the heat exchanged with the outside by the component is equal to the change in enthalpy of the fluid passing through it.

This fundamental relationship explains why, in industrial devices, it is virtually impossible to implement both great mechanical work and a significant heat flux.

• Components which transfer heat from one fluid to another require large exchange areas, their heat fluxes being proportional to them. Technical and economic considerations lead to the adoption of purely static devices,  for example, large bundles of tubes in parallel, traversed internally by a fluid while the other flows outside. is zero because of the absence of movable walls.

• Machines doing the compression or expansion of a fluid have a very compact design for reasons of weight, size and cost. For similar reasons, they rotate very fast (several thousand revolutions per minute). Each parcel of fluid remains there very shortly. Moreover, the heat exchange coefficients of gases have low values. Short residence time, small areas of fluid-wall contact, and low exchange coefficients imply that the heat exchange is minimal and that the operation of these machines is nearly adiabatic.

• There is a class of devices where and Q are both zero: they are static expanders such as valves, filters etc. The corresponding process is called an isenthalpic throttling or a flash expansion.

In summary, the application of this equation leads to the following conclusions:

• in a heat exchanger, heat Q transferred or provided by one fluid to another is equal to its enthalpy change Δh;

• in an adiabatic machine, shaft work is equal to the change in enthalpy of the fluid Δh ;

• throttling conserves enthalpy (Δh = 0).

For the calculation of processes, these findings are very important in practice since they indicate that in most components of industrial machinery, mechanical and thermal exchanges are decoupled. They also explain why the enthalpy is a state function widely used in open system processes: the change in enthalpy of the fluid represents the mechanical or thermal energy put in.