Dans sa forme la plus simple et la plus répandue, une turbine à gaz est composée de trois éléments :

• un compresseur, généralement centrifuge ou axial, qui a pour rôle de comprimer de l'air ambiant à une pression comprise aujourd'hui entre 10 et 30 bars environ ;

• une chambre de combustion, dans laquelle du combustible injecté sous pression est brûlé avec l'air comprimé, avec un fort excès d'air afin de limiter la température des gaz d'échappement ;

• une turbine, généralement axiale, dans laquelle sont détendus les gaz qui sortent de la chambre de combustion.

Sous cette forme, la turbine à gaz constitue un moteur à combustion interne à flux continu. On notera que le terme de turbine à gaz provient de l'état du fluide de travail, qui reste toujours gazeux, et non du combustible utilisé, qui peut être aussi bien gazeux que liquide (les turbines à gaz utilisent généralement du gaz naturel ou du fuel oil domestique). Il existe aussi des turbines à gaz à cycle fermé, utilisées pour des applications particulières. Bien évidemment, il s'agit alors de moteurs à combustion externe.

L'étude thermodynamique d'un tel cycle, appelé cycle de Brayton, peut être effectuée de différentes manières, selon le niveau des élèves et le parti-pris pédagogique de l'enseignant.

Il est bien évidemment possible de modéliser directement ce cycle dans Thermoptim en faisant très peu d'hypothèses simplificatrices. Nous ne détaillerons pas ici complètement cette manière d'opérer, qui est bien documentée dans le guide de prise en mains relatif à la turbine à gaz ou bien dans la séance Diapason S24 .

Une question importante est de savoir s'il faut commencer par prendre en compte la réaction de combustion. Dans ce qui suit, nous considérerons que, ce chapitre étant destiné à présenter les activités d'initiation, il est préférable de ne pas le faire, afin de simplifier la modélisation. Dans ce cas, la chambre de combustion est remplacée par un échangeur qui permet de chauffer l'air à la température d'entrée turbine désirée.

Il est alors possible d'effectuer la modélisation progressivement, en opérant comme suit :

• on commence par faire l'hypothèse que la machine est traversée par un gaz unique, l'air, modélisé dans un premier temps comme un gaz parfait, et dans un deuxième temps comme un gaz idéal. Le modèle qui en résulte est bien évidemment simpliste, mais il reste intéressant sur le plan didactique, car il permet de faire le lien entre les calculs théoriques analytiques et leur résolution précise ;

• on ne tient compte qu'ensuite de la réaction de combustion qui prend place dans les machines industrielles, ce qui permet d'élaborer un modèle beaucoup plus réaliste. La comparaison avec le modèle analytique permet d'en analyser les limites.

Les séances Diapason S21 et S22 correspondent à des modélisations directes dans Thermoptim retenant précisément cette approche.

Nous en donnerons seulement ici un bref aperçu, après avoir présenté une manière de faire qui peut convenir à des élèves débutants si l'enseignant souhaite qu'ils comprennent bien la manière dont les calculs sont effectués. Nous montrerons comment les élèves peuvent calculer le cycle pas à pas en procédant de deux manières différentes : tout d'abord en utilisant le calculateur-inverseur des propriétés des fluides, qui permet de ne pas faire appel à Thermoptim dans un premier temps, et ensuite en créant des points dans le progiciel. Une fois les points du cycle déterminés, ils peuvent être tracés dans le diagramme entropique.

Cette manière de faire, qui diffère de la modélisation directe dans Thermoptim, présente sur le plan pédagogique l'intérêt que la démarche méthodologique de calcul d'un cycle doit être suivie de manière plus détaillée. Sa limite est que la combustion ne peut être prise en compte correctement.

1. l'air est aspiré à la pression et à la température ambiantes, puis comprimé à une pression comprise entre 10 et 30 bars : évolution (1-2). Cette compression peut en première approximation être supposée adiabatique, pour les raisons évoquées dans l'introduction, mais pas isentropique, compte tenu des irréversibilités qui prennent place dans le compresseur. A la différence du cycle de Hirn ou de Rankine, utilisé dans les centrales à vapeur et dans lequel le travail de compression est faible devant le travail de détente, une partie significative (60 à 70 %) du travail récupéré sur l'arbre de la turbine sert ici à entraîner le compresseur ;

2. l'air sous pression est ensuite dirigé vers la chambre de combustion (évolution 2-3), où il brûle avec un combustible (distillat léger, gaz naturel). Il faut aussi bien noter que la machine met en jeu plusieurs fluides : de l'air, dont le débit-masse est pris égal à l'unité, un combustible, dont le débit-masse est calculé par la chambre de combustion, et les gaz brûlés, dont on déduit le débit-masse par bilan conservatif. La chambre de combustion est un dispositif fixe. Les pertes de charge y étant très faibles, elle est en première approximation isobare ;

3. les gaz brûlés sont ensuite détendus dans une turbine de rendement isentropique voisin de 0,9, jusqu'à la pression atmosphérique : évolution (3-4).

Le schéma de la machine (figure ci-dessous) se déduit de ces considérations.

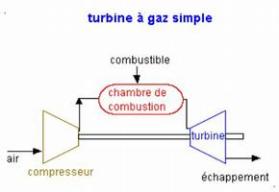
L'exemple proposé ici correspond à l'énoncé suivant : une turbine à gaz brûlant du gaz naturel sans dissociation aspire de l'air à 15 °C et 1 bar et le comprime à 16 bars dans un compresseur de rendement polytropique 0,85, puis les gaz brûlés sont détendus dans une turbine de rendement polytropique 0,85. La température d'entrée dans la turbine est de 1150 °C.

Si l'enseignant préfère ne pas introduire tout de suite la notion de rendement poytropique, il peut être reformulé sous la forme : une turbine à gaz brûlant du gaz naturel sans dissociation aspire de l'air à 15 °C et 1 bar et le comprime à 16 bars dans un compresseur de rendement isentropique 0,787, puis les gaz brûlés sont détendus dans une turbine de rendement isentropique 0,89. La température d'entrée dans la turbine est de 1150 °C.

Une fois le schéma de principe de la machine ainsi défini, la discussion peut porter sur les technologies des divers composants.

Pour atteindre des taux de compression r de 20 ou 30, le compresseur est multiétagé, avec parfois une réfrigération intermédiaire destinée à réduire le travail consommé. Les rotors axiaux sont constitués d'un empilage de disques, soit montés sur un moyeu central, soit assemblés en tambour sur leur périphérie. Les matériaux utilisés vont des alliages d'aluminium ou de titane pour les premiers étages aux alliages d'acier et aux alliages réfractaires pour les derniers étages, qui peuvent supporter des températures atteignant 500 °C.

La chambre de combustion est normalement construite en alliage réfractaire. Elle doit satisfaire des contraintes sévères :

• assurer une combustion complète du combustible ;

• réduire les émissions de polluants ;

• minimiser la perte de charge (qui représente un surcroît de compression) ;

• assurer une bonne stabilité de la température d'entrée turbine ;

• occuper un volume aussi réduit que possible tout en permettant un bon refroidissement des parois.

Dans les turbines à gaz à cycle ouvert, les principales contraintes technologiques se situent au niveau des premiers étages de la turbine de détente, qui sont soumis au flux des gaz d'échappement à très haute température. Les pièces les plus exposées sont en particulier les aubages du rotor, qui sont très difficiles à refroidir et, de plus, particulièrement sensibles à l'abrasion. Il importe donc d'utiliser un combustible très propre (absence de particules et de composants chimiques susceptibles de former des acides), et de limiter la température en fonction des caractéristiques mécaniques des aubages.

Les matériaux utilisés pour les aubages de la turbine sont des alliages réfractaires à base de nickel ou de cobalt, et on envisage de recourir à des céramiques dans l'avenir.

Comme le rendement du cycle est lui-même une fonction croissante de la température, d'importants développements technologiques ont été consacrés à la mise au point, d'une part de systèmes de refroidissement efficaces des aubages, et d'autre part de matériaux résistant aux températures élevées. Depuis un demi-siècle, on a ainsi pu relever progressivement (d'environ 20 °C par an) le niveau de température d'entrée dans la turbine, pour atteindre aujourd'hui 1300 à 1500 °C.

Deux grandes catégories de turbines à gaz sont généralement distinguées : les turbines à gaz industrielles, lourdes et robustes, mais de performances moyennes (rendement 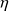entre 28 et 38 %), et les turbines à gaz "dérivées de l'aviation" ou "aérodérivées", beaucoup plus légères et performantes ( 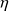entre 35 et 42 %), mais aussi plus chères (figure ci-dessous).

Les puissances des premières vont de quelques dizaines de kW (microturbines) à quelques centaines de MW, alors que celles des machines aérodérivées sont généralement comprises entre quelques centaines de kW et quelques dizaines de MW, correspondant à celles des moteurs aéronautiques. La plupart des turboréacteurs utilisés aujourd'hui dans l'aviation ne sont en fait que des variantes de la turbine à gaz à cycle ouvert. Le marché de l'aviation a ainsi permis de financer d'importants programmes de développement technologique sur ces moteurs, qui ont abouti à la mise au point de turbines à gaz extrêmement performantes, susceptibles de supplanter les turbines à gaz industrielles, ou de permettre la conception de turbines composées, de rendements améliorés et à faible coût, comprenant des composants de turboréacteurs existants pour les sections haute pression du compresseur et de la turbine, et des pièces industrielles pour les sections basse pression.

Pour calculer ce cycle pas à pas, nous commencerons par utiliser le calculateur inverseur, sachant que le principal intérêt qu'il y a à procéder ainsi est d'une part de bien décomposer les différentes étapes et d'autre part de ne pas avoir dans un premier temps à introduire Thermoptim. Comme nous l'avons indiqué, nous retiendrons une approche progressive où nous commencerons par étudier le cycle à air parfait, puis celui à air idéal.

3.3.1 ETAT DU POINT 1

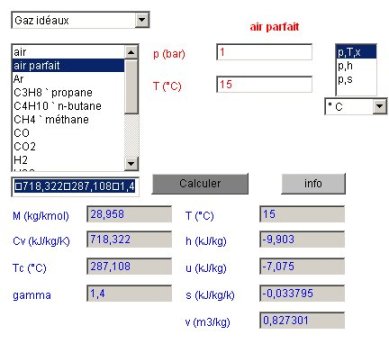
L'état du point 1 correspond au paramétrage du calculateur conformément à la figure donnée ci-dessous. Le fluide sélectionné est l'air parfait, parmi les gaz idéaux. Précisons qu'il s'agit d'un corps fictif, qui présente la particularité d'avoir la même masse molaire que l'eau et une valeur de 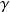égale à 1,4. Le calculateur doit être en mode de calcul (p,T,x) la pression étant égale à 1 bar, et la température à 15 °C. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes (p est en bar, h, u, r et Cv en kJ/kg, s en kJ/kg/K, v en m3/kg, M en kg :

3.3.2 ETAT DU POINT 2s

Pour connaître l'état du point 2s, correspondant à la compression isentropique, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant égale à 16 bars, et l'entropie étant celle du point 1. Le calcul conduit à la figure ci-dessous.

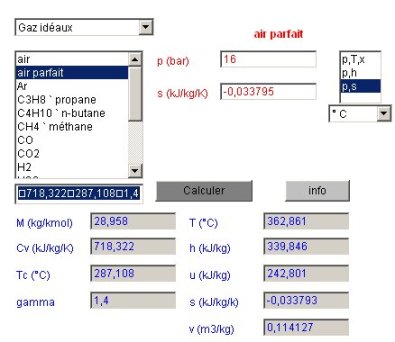
Un copier-coller depuis le champ des résultats fournit les valeurs suivantes, la valeur de l'entropie différant très légèrement du fait de la précision d'inversion des calculs.

La variation d'enthalpie correspondant à la détente réversible est égale à h2s – h1, soit 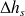= 349,749 kJ/kg. Sa valeur positive provient des conventions utilisées en thermodynamique, le travail étant reçu de l'extérieur du système considéré.

La valeur du travail de compression réel est, par définition du rendement isentropique 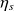, égal à 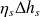soit :

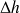= 349,749/0,787 kJ/kg = 444,4079 kJ/kg

L'enthalpie du point 2 est donc égale à celle du point 1 plus 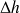, soit 434,505 kJ/kg

3.3.3 ETAT DU POINT 2

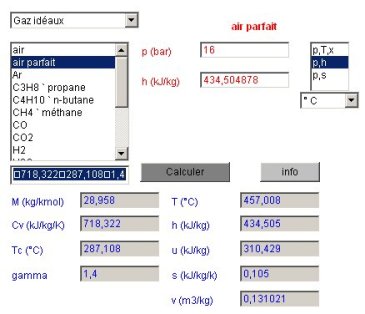
Pour connaître l'état du points 2, le calculateur doit être paramétré en mode de calcul (p,h) la pression restant égale à 16 bars, et l'enthalpie étant 434,505. Le calcul conduit à la figure ci-dessous, et un copier-coller depuis le champ des résultats fournit les valeurs suivantes  :

3.3.4 ETAT DU POINT 3

Pour connaître l'état du point 3, le calculateur doit être en mode de calcul (p,T,x) la pression restant égale à 16 bars, et la température valant 1150 °C. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

La chaleur Q à fournir par la chambre de combustion est égale à la variation d'enthalpie entre les points 2 et 3 : Q = 696,754 kJ/kg.

3.3.5 ETAT DU POINT 4s

Pour connaître l'état du points 4s, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant celle d'échappement, égale à 1 bar, et l'entropie étant celle du point 3. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

La valeur du travail de détente réel 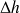est, par définition du rendement isentropique 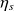, égal à 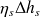soit :

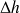= 0,89 (- 782,608) kJ/kg = - 696,52112 kJ/kg

L'enthalpie du point 4 est donc égale à celle du point 3 plus 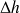(en valeur algébrique), soit 434,73788 kJ/kg

3.3.6 ETAT DU POINT 4

Pour connaître l'état du points 4, le calculateur doit être paramétré en mode de calcul (p,h) la pression restant égale à 1 bar, et l'enthalpie étant celle du point 4. Le calcul conduit à la figure ci-dessous.

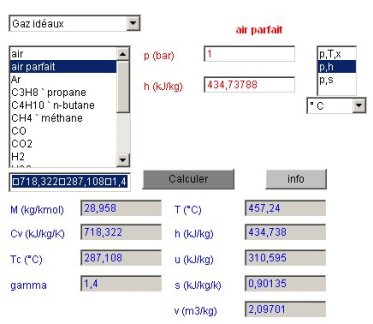
Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

3.3.7 BILAN GLOBAL DU CYCLE

Les calculs précédents ont permis d'estimer la chaleur Q fournie par la chaudière (696,754 kJ/kg), et le travail net est égal en valeur absolue à la différence entre celui produit par la turbine (696,52 kJ/kg) et celui consommé par le compresseur (444,41 kJ/kg), soit 252,11 kJ/kg.

Le rendement du cycle est égal au rapport de ces deux valeurs. Il vaut donc 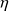= 252,11/696,75 = 36,18 %.

3.3.8 COMPARAISON AVEC LES CALCULS ANALYTIQUES

A ce stade, il peut être intéressant de proposer aux élèves de comparer les résultats obtenus avec ceux auxquels conduisent les calculs analytiques de la compression et de la détente isentropiques (figure ci-dessous). Le document joint intitulé CalculsAnalytiquesTAG.pdf montre que les résultats obtenus sont bien les mêmes.

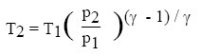
L'intérêt de cette comparaison est que les élèves peuvent constater par eux-mêmes que le calculateur-inverseur fournit bien les mêmes résultats que les équations qui lui ont été enseignées pour les calculs simples qui peuvent être menés analytiquement.

3.3.9 PRISE EN COMPTE DE L'INFLUENCE DE LA TEMPERATURE SUR LE Cp DE L'AIR

Dans les calculs qui ont été effectués jusqu'ici, l'air a été supposé parfait, alors qu'en fait sa capacité thermique massique Cp varie avec la température. Pour pouvoir estimer l'influence de cette dépendance, il est possible de recalculer l'ensemble du cycle en considérant que le corps est maintenant de l'air et non de l'air parfait.

3.3.9.1 ETAT DU POINT 1

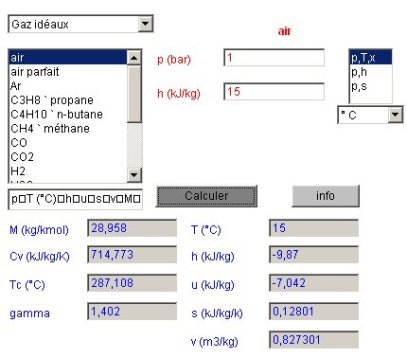
L'état du point 1 correspond au paramétrage du calculateur conformément à la figure du calculateur donnée ci-dessous. Le fluide sélectionné est l'air, parmi les gaz idéaux. Le calculateur doit être en mode de calcul (p,T,x) la pression étant égale à 1 bar (on néglige la différence avec une atmosphère), et la température égale à 15 °C. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

3.3.9.2 ETAT DU POINT 2s

Pour connaître l'état du point 2s, correspondant à la compression isentropique, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant égale à 16 bars, et l'entropie étant celle du point 1. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

La variation d'enthalpie correspondant à la détente réversible est égale à h2s – h1, soit 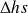= 348,472 kJ/kg.

La valeur du travail de compression réel est, par définition du rendement isentropique 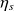, égal à 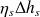soit :

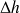= 348,472/0,787 kJ/kg = 442,7852605 kJ/kg

L'enthalpie du point 2 est donc égale à celle du point 1 plus 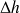, soit 432,915 kJ/kg

3.3.9.3 ETAT DU POINT 2

Pour connaître l'état du points 2, le calculateur doit être paramétré en mode de calcul (p,h) la pression restant égale à 16 bars, et l'enthalpie étant 432,915. Le calcul conduit à la figure ci-dessous, et un copier-coller depuis le champ des résultats fournit les valeurs suivantes  :

3.3.9.4 ETAT DU POINT 3

Pour connaître l'état du point 3, le calculateur doit être en mode de calcul (p,T,x) la pression restant égale à 16 bars, et la température valant 1150 °C. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

La chaleur Q à fournir par la chambre de combustion est égale à la variation d'enthalpie entre les points 2 et 3 : Q = 812,2894 kJ/kg.

3.3.9.5 ETAT DU POINT 4s

Pour connaître l'état du points 4s, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant celle d'échappement, égale à 1 bar, et l'entropie étant celle du point 3. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

La valeur du travail de détente réel 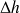est, par définition du rendement isentropique 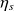, égal à 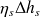soit :

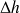= 0,89 (- 820,696) kJ/kg = - 730,41944 kJ/kg

L'enthalpie du point 4 est donc égale à celle du point 3 plus 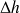(en valeur algébrique), soit 514,78456 kJ/kg

3.3.9.6 ETAT DU POINT 4

Pour connaître l'état du points 4, le calculateur doit être paramétré en mode de calcul (p,h) la pression restant égale à 1 bar, et l'enthalpie étant celle du point 4.

Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :

3.3.9.7 BILAN GLOBAL DU CYCLE

Les calculs précédents ont permis d'estimer la chaleur Q fournie par la chaudière (812,2894 kJ/kg), et le travail net est égal en valeur absolue à la différence entre celui produit par la turbine (730,419 kJ/kg) et celui consommé par le compresseur (442,785 kJ/kg), soit 287,634 kJ/kg.

Le rendement du cycle est égal au rapport de ces deux valeurs. Il vaut donc 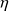= 287,634/812,28945 = 35,41 %.

Entre les deux modèles, la différence est assez faible en terme de rendement, mais beaucoup plus importante en terme de température d'échappement des gaz, 518 °C au lieu de 457 °C, ou de puissance de la machine 287 kW au lieu de 252.

Les écrans des points de Thermoptim permettent de faire les mêmes calculs que ceux que nous venons d'effectuer. Comme nous allons le voir, les résultats sont identiques, mais cela suppose de tout de suite initier les élèves à une partie des fonctionnalités du simulateur.

Tant que l'on ne définit pas les transfos, l'éditeur de schémas ne doit pas être utilisé. Les points peuvent en effet être directement créés depuis l'écran du simulateur, en double-cliquant sur le bandeau de la table des points. Une fois qu'un point existe, le bouton « Dupliquer » permet d'en générer un autre sans avoir à entrer le corps.

Dans ce qui suit, nous travaillerons directement avec de l'air, sans traiter le cas de l'air parfait, afin d'éviter des redites.

3.4.1 ETAT DU POINT 1

L'état du point 1 est donné figure ci-dessous. La pression et la température doivent être entrées.

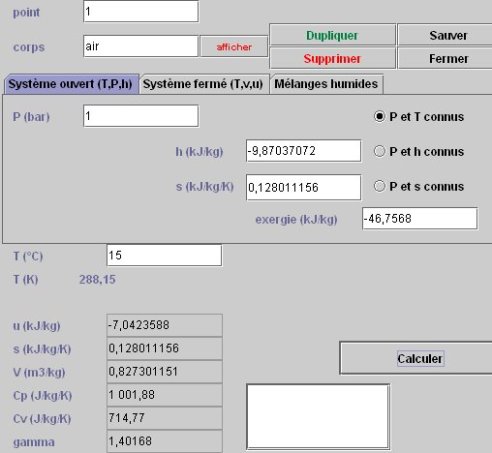
3.4.2 ETAT DU POINT 2s

Pour connaître l'état du point 2s, le point doit être paramétré en mode de calcul « P et s connus », la nouvelle pression étant égale à 16 bars, et l'entropie étant celle du point 1. Le calcul conduit à la figure ci-dessous.

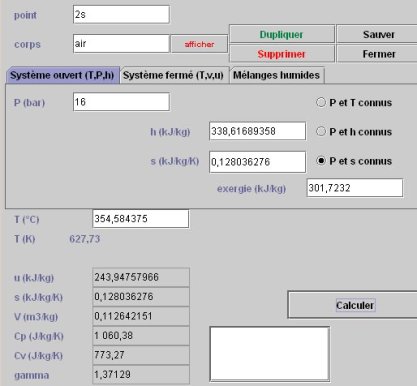
La variation d'enthalpie correspondant à la détente réversible est égale à h2s – h1, soit 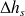= 348,472 kJ/kg. La valeur du travail de compression réel est, par définition du rendement isentropique 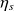, égal à 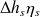soit :

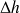= 348,472/0,787 kJ/kg = 442,7852605 kJ/kg

L'enthalpie du point 2 est donc égale à celle du point 1 plus 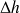, soit 432,915 kJ/kg

3.4.3 ETAT DU POINT 2

Pour connaître l'état du point 2, le point doit être paramétré en mode de calcul « P et h connus », la nouvelle pression étant égale à 16 bars, et l'enthalpie valant 432,915 kJ/kg. Le calcul conduit à la figure ci-dessous.

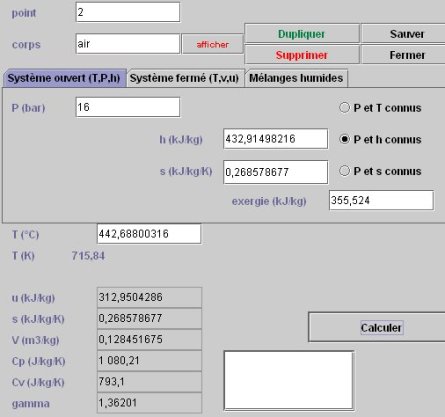
3.4.4 ETAT DU POINT 3

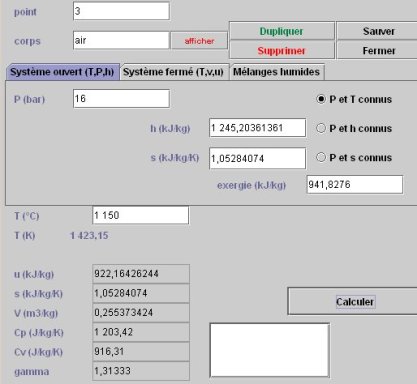
Pour connaître l'état du point 3, le paramétrage doit être « P et T connus », la pression restant égale à 16 bars, et la température valant 1150 °C.

La chaleur Q à fournir par la chambre de combustion est égale à la variation d'enthalpie entre les points 2 et 3 : Q = 812,2894 kJ/kg.

3.4.5 ETAT DU POINT 4s

Pour connaître l'état du points 4s, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant celle d'échappement, égale à 1 bar, et l'entropie étant celle du point 3.

La valeur du travail de détente réel 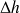est, par définition du rendement isentropique 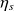, égal à 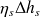soit :

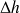= 0,89 (- 820,696) kJ/kg = - 730,41944 kJ/kg

L'enthalpie du point 4 est donc égale à celle du point 3 plus 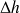(en valeur algébrique), soit 514,78456 kJ/kg

3.4.6 ETAT DU POINT 4

Pour connaître l'état du point 4, le paramétrage doit être « P et h connus », la pression restant égale à 1 bar, et l'enthalpie étant celle du point 4. Le calcul conduit à la figure ci-dessous.

3.4.7 BILAN GLOBAL DU CYCLE

Les points étant les mêmes que ceux qui avaient été déterminés avec le modèle dont le corps était de l'air, le bilan du cycle est bien le même.

La modélisation directe du cycle dans Thermoptim est celle qui est présentée de manière détaillée dans la séance Diapason S21. Nous nous contenterons ici d'en rappeler les grandes lignes.

3.5.1 CREATION DU SCHEMA

Dans cette approche, l'élève commence par travailler avec l'éditeur de schémas, plaçant les différents composants sur la palette et saisissant pour chacun d'eux un tout petit nombre d'informations. Il aboutit ainsi à un schéma du type de celui présenté figure ci-dessous, qu'il transfère dans le simulateur : il ne diffère du schéma-bloc qu'au niveau de la chambre de combustion remplacée par une transfo-échange.

3.5.2 PARAMETRAGE DU CYCLE

Dans un second temps, l'élève paramètre sur le plan thermodynamique les points dont l'état est parfaitement connu (1 et 3), et les transfos compression et détente, ce qui permet de calculer les deux autres points.

3.5.3 COMPARAISON DES DEUX APPROCHES PEDAGOGIQUES

L'intérêt de la modélisation directe dans Thermoptim est qu'elle se fait dans un premier temps dans l'éditeur de schémas, l'architecture du cycle étant très proche de celle du schéma-bloc.

L'élève commence donc par réfléchir à la structure globale du cycle, sans avoir à se préoccuper de la manière dont les calculs sont effectués dans chaque composant. La modélisation est grandement facilitée, ce qui est un atout sur le plan psychologique, car l'élève est vraiment convaincu que le simulateur lui permet de "faire de la thermo sans peine". Il est donc encouragé à continuer, ses appréhensions initiales vis à vis de la discipline s'estompant.

Le risque est qu'il ait tendance à utiliser le logiciel de façon « presse-bouton », sans bien comprendre la méthodologie sous-jacente. Le parti pris pédagogique est donc assez différent de celui qui a été retenu dans les sections 3.3 et 3.4, où l'enseignant considère fondamental que l'élève ait pleinement conscience de l'enchaînement des calculs.

Dans tous les cas, les calculs sont effectués par un logiciel, ce qui correspond bien au même paradigme global, celui de la réduction des difficultés calculatoires, mais le degré d'implication de l'élève n'est pas le même. Les deux approches pédagogiques constituent donc des variantes entre lesquelles l'enseignant choisira, en fonction du contexte auquel il est confronté.

3.5.4 PRISE EN COMPTE DE LA COMBUSTION

Jusqu'à présent, nous n'avons pas tenu compte de la combustion de manière précise, la chambre de combustion étant remplacée par un échauffement de l'air. Le calculateur-inverseur ne permet en effet pas de définir un gaz composé correspondant aux fumées.

La modélisation complète dans Thermoptim est expliquée dans le guide de prise en mains et dans la séance Diapason S24. Elle suppose de remplacer la transfo échange de la figure ci-dessus par une chambre de combustion et une transfo-point représentant l'entrée de combustible, le schéma correspondant à la figure ci-dessous.

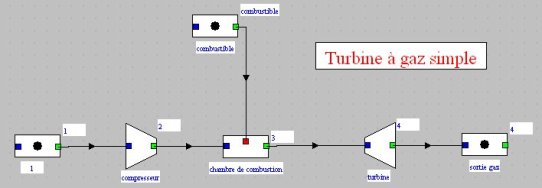
Le modèle précis avec combustion conduit à une température de sortie turbine égale à 533 °C, une puissance thermique de 889 kW, une puissance mécanique nette de 318 kW et un rendement de 35,8 %, soit des valeurs dont l'écart avec celles du modèle à gaz idéal (respectivement 518 °C, 812 kW, 287 kW et 35,4 %) est plus réduit qu'entre ce dernier et le modèle où l'air était considéré comme un gaz parfait (respectivement 457 °C, 697 kW, 252 kW et 36,1 %).

Une fois les points du cycle déterminés, il est possible de le tracer dans le diagramme entropique.

Dans ce qui précède, nous avions introduit les points 2s et 4s, intermédiaires qui n'ont pas besoin d'être représentés.

Si le cycle a été calculé en créant des points dans Thermoptim, comme expliqué dans les sections 3.3 ou 3.5, leur tracé dans les diagrammes peut être directement effectué en utilisant l'interface entre le simulateur et les diagrammes. S'il a été calculé avec le calculateur-inverseur, il faut commencer par créer les points dans le simulateur.

3.6.1 SAISIE DIRECTE DES POINTS DANS L'EDITEUR DE CYCLES

Il est possible d'enter directement les points dans l'éditeur de cycles du diagramme, en opérant de la manière suivante.

Une fois le diagramme des gaz idéaux ouvert pour l'air, l'éditeur de cycles est accessible à partir du menu Cycle ou en tapant Ctrl C (figure ci-dessous).

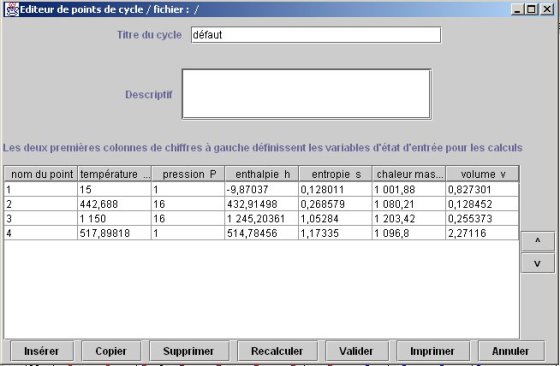
En utilisant le bouton Insérer, il est alors possible d'entrer les différents points un par un. La seule contrainte est que, le bouton de recalcul n'étant pas disponible dans la version Education Salle de cours de Thermoptim, il faut entrer à la main toutes les valeurs des variables (T, P, s et h) pour que le cycle soit correctement construit.

Notons qu'une fois ces points créés dans l'environnement des diagrammes, il est possible de les transférer dans le simulateur en utilisant l'interface qui les relie.

Dans l'écran de l'interface (figure ci-dessous), il faut commencer par mettre à jour la table des points, puis mettre à jour le simulateur à partir du diagramme.

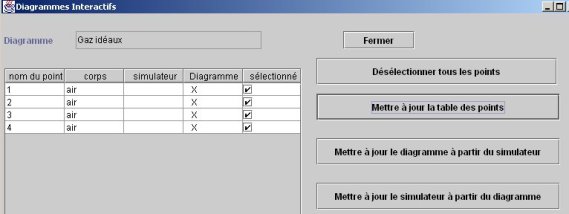
Les points sont alors créés dans le simulateur. Une fois ce transfert effectué, il est toutefois préférable de reprendre les paramétrages des points un par un.

3.6.2 TRACE DANS LE DIAGRAMME ENTROPIQUE

Le tracé du cycle dans le diagramme entropique est donné dans la figure ci-dessous.

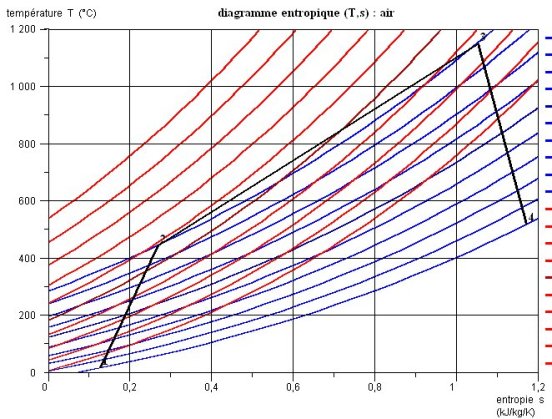
Compte tenu de la forme des isobares dans le diagramme entropique (proches d'exponentielles), l'écart est important pour cette évolution par rapport au cycle de Carnot qui stipule que la machine thermique échange de la chaleur à température constante avec la source chaude.

Un autre point à bien souligner est que, dans la machine réelle, le fluide thermodynamique change de composition lors de cette évolution, de telle sorte qu'en toute rigueur le tracé du cycle ne peut être fait dans un seul diagramme. On pourra d'ailleurs faire vérifier aux élèves que le tracé dans le diagramme entropique du cycle avec combustion conduit apparemment à une erreur en ce sens que les points 2 et 3 ne sont pas situés sur la même isobare. Cela vient de ce que l'entropie du point 3 est augmentée du fait de la réaction de combustion, et apparaît ainsi décalée dans le diagramme entropique.

Si le cycle a été modélisé sans utiliser l'éditeur de schémas de Thermoptim, (cf. sections 3.3 et 3.4), et que les points du cycle ont été créés ou transférés dans le simulateur afin de pouvoir les représenter dans les diagrammes, le projet se présente comme indiqué figure ci-dessous.

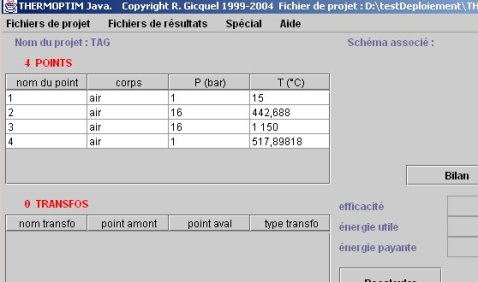
Pour finir de représenter le cycle dans Thermoptim, il faut maintenant relier ces points par des transfos, ce qui peut être fait très simplement à partir de l'éditeur de schémas. Il suffit pour cela de sélectionner dans la palette les différents composants, en entrant dans les champs définissant les ports d'entrée et de sortie leurs différents noms et leur corps (de l'air).

Les points étant tous connus, les transfos doivent être initialement paramétrées en conséquence. En particulier le compresseur et la turbine doivent recalculer la valeur du rendement, le point aval étant connu.

Une fois ces valeurs déterminées, le paramétrage peut être changé si l'on désire pouvoir simuler d'autres cas.

Autour du cycle de turbine à gaz, de nombreuses activités intéressant les élèves peuvent prendre place :

• comparer qualitativement ce cycle par rapport au cycle de Carnot, en identifiant les écarts qui existent entre eux ;

• réfléchir sur la notion d'efficacité du cycle, égale au rapport de l'énergie utile (ici la somme algébrique du travail de détente et du travail de compression) à l'énergie payante (ici la chaleur fournie dans la chambre de combustion) ;

• comparer cette valeur avec celle du cycle de Carnot fonctionnant entre 15 °C (source froide) et 1150 °C (température maximale du cycle), pour se faire une idée de l'écart du cycle réel (0,354) par rapport au cycle idéal (0,797) ;

• étudier l'évolution de l'efficacité du cycle et de la puissance produite lorsque la pression et la température maximales varient. En faisant varier la pression du cycle, on obtient un abaque donnant l'évolution du rendement en fonction du travail utile^[1]. Le rendement maximum est obtenu, à température d'entrée turbine donnée, pour un certain rapport de compression, et la puissance maximale pour un autre ;

• la plupart des turbines à gaz travaillent en cycle ouvert et rejettent dans l'atmosphère des gaz à température élevée (500 - 600 °C). Il peut quelquefois être possible d'améliorer le cycle en ayant recours à la régénération, c'est-à-dire en valorisant les gaz d'échappement en préchauffant l'air en sortie du compresseur. Une discussion sur les limites de cette solution fournit l'occasion d'un échange fructueux avec les élèves ;

• une autre manière d'améliorer le cycle consiste à injecter de la vapeur formée en utilisant les gaz d'échappement pour vaporiser de l'eau comprimée à l'état liquide.

Dans ce qui précède, nous avons montré comment calculer pas à pas le cycle de la turbine à gaz, puis comment le modéliser dans Thermoptim, en partant du principe que l'objectif pédagogique visé était d'apprendre aux élèves à acquérir ce savoir-faire tout en assimilant des connaissances déclaratives suffisantes pour comprendre les fondements de ces opérations.

Il existe cependant des contextes pédagogiques où cette manière de procéder ne peut pas être adoptée, essentiellement par manque de temps, et où cependant l'enseignant souhaite que ses élèves puissent utiliser Thermoptim et les diagrammes interactifs, sans construire par eux-mêmes les modèles.

C'est par exemple le cas dans certaines Classes Préparatoires aux Grandes Ecoles (CPGE) où le volume horaire est insuffisant pour opérer comme nous l'avons fait dans les sections précédentes. Pourtant, de nombreux enseignants considèrent pédagogiquement pertinent d'utiliser Thermoptim, car cela permet aux élèves de voir comment les équations qu'ils étudient peuvent être mises en application. Leur programme acquiert ainsi dans leur esprit davantage de sens : il correspond à un savoir qui peut être vraiment utilisé.

Dans de tels cas, une alternative pédagogique à celles que nous avons présentées jusqu'ici consiste à faire travailler les élèves sur des exemples déjà modélisés, en leur demandant de les explorer et de les comprendre. Ils peuvent aussi modifier les paramétrages et réaliser quelques études de sensibilité.

S'il souhaite faire étudier la turbine à gaz simple de cette manière, l'enseignant sélectionne alors dans le catalogue d'exemples de Thermoptim l'exemple intitulé "t1_6.3 turbine à gaz simple" à partir du catalogue d'exemples et demande à ses élèves de le charger.

Le projet étant chargé, il commence par passer en revue les différents composants, en fournissant à ses élèves des explications technologiques et thermodynamiques. Ensuite, il peut leur demander de procéder à des changements de paramétrage et d'en étudier l'impact sur les performances globales du cycle.

Même si elle peut paraître un peu limitée, cette approche pédagogique peut se révéler très féconde, les élèves s'impliquant souvent beaucoup plus lorsqu'ils ont un simulateur à leur disposition que devant une feuille de papier ou un tableau. Elle est en particulier souvent appropriée en formation professionnelle, les élèves étant généralement assez réticents devant les approches disciplinaires académiques. Ils préfèrent avoir l'outil logiciel entre leurs mains pour pouvoir l'explorer à leur guise et poser des questions aux enseignants qui les encadrent.