Dans un premier temps, tant que les élèves n'ont pas acquis une culture suffisante du domaine, il nous semble préférable :

• d'une part de privilégier une compréhension des performances globales des composants, en s'attachant à mettre en évidence les expressions des grandeurs caractéristiques représentatives de leur fonctionnement d'ensemble, ce qui permet d'éluder les difficultés auxquelles conduirait une modélisation détaillée ;

• d'autre part de ne pas trop insister sur la démarche systémique qui sous-tend la modélisation avec Thermoptim. Les notions correspondantes seront plus faciles à comprendre lorsque les élèves auront acquis une certaine expérience de la modélisation, lors des activités de consolidation (cf. troisième partie).

Pour commencer, un rappel de l'expression enthalpique du premier principe est souhaitable, en expliquant bien aux élèves que les cycles qui seront considérés ici, bien que globalement fermés, sont formés de plusieurs transformations réalisées pour chacune d'elles en système ouvert^[1].

Les notations sont celles de la référence [1].

C étant la vitesse du fluide, le premier principe appliqué à un composant traversé par un débit unitaire de fluide s'exprime, en unités massiques, sous la forme :

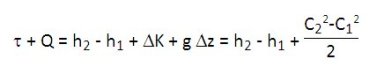
Pour la plupart des machines thermiques, le terme 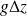  est négligeable. Dans de nombreux cas, la variation d'énergie cinétique 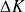reste faible vis à vis des autres variations (sauf bien entendu dans des cas spéciaux tels que les réacteurs d'avion, certains aubages de turbomachines ou organes de détente).

Dans ces conditions, la somme du travail reçu ou fourni et de la chaleur échangée avec l'extérieur par le composant est égale à la variation d'enthalpie du fluide qui le traverse.

Cette relation fondamentale explique pourquoi, dans les appareils industriels, il est pratiquement impossible de mettre en œuvre à la fois une forte puissance mécanique et un flux calorifique important.

Pour le calcul des transformations, les implications de ce constat sont très importantes en pratique puisqu'elles indiquent que dans la plupart des composants des machines industrielles, les échanges thermiques et mécaniques sont découplés. Elles expliquent aussi pourquoi l'enthalpie est une fonction d'état^[2] très utilisée dans les transformations en système ouvert^[1] : la variation d'enthalpie du fluide correspond selon les cas à l'énergie mécanique ou thermique mise en jeu.

1.1.1 ECHANGEURS DE CHALEUR

Les composants appelés à transférer de la chaleur d'un fluide à un autre nécessitent de grandes surfaces d'échange, les flux thermiques leur étant proportionnels. Des considérations techniques et économiques amènent à adopter des dispositifs purement statiques. Par exemple, de grands faisceaux de tubes en parallèle, parcourus intérieurement par un fluide pendant que l'autre circule à l'extérieur.

est alors nul en raison de l'absence de parois mobiles.

En première approximation, ces échangeurs peuvent être supposés isobares.

Dans un échangeur de chaleur, la chaleur Q cédée ou fournie par un fluide à l'autre est égale à sa variation d'enthalpie .

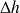1.1.2 CHAMBRES DE COMBUSTION, CHAUDIERES

Le même raisonnement s'applique aux chambres de combustion ou aux chaudières, qui peuvent généralement être considérées comme isobares. La combustion a donc lieu à pression constante, ce qui surprend toujours un certain nombre d'élèves, convaincus que la combustion élève la pression, même en système ouvert^[1].

Dans une chambre de combustion ou une chaudière, la chaleur Q cédée au fluide qui la traverse est égale à sa variation d'enthalpie .

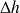1.1.3 COMPRESSEURS ET TURBINES

Les machines réalisant la compression ou la détente d'un fluide ont une conception très compacte pour des raisons de poids, d'encombrement et de coût. Pour les mêmes raisons, elles tournent très vite (plusieurs milliers de tours par minute). Chaque parcelle de fluide y séjourne très peu de temps.

Par ailleurs les coefficients d'échange thermique des gaz ont des valeurs faibles.

Les courts temps de séjour, les petites surfaces de contact fluide-paroi, et les faibles coefficients d'échange font que l'échange de chaleur est minime et que le fonctionnement de ces machines est pratiquement adiabatique.

Dans une machine adiabatique de compression ou détente, le travail utile^[3] est égal à la variation d'enthalpie du fluide .

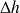Il faut bien insister auprès des élèves sur le fait que, bien que la machine puisse être considérée comme adiabatique, des irréversibilités y prennent généralement place, de telle sorte que son fonctionnement n'est pas isentropique. L'isentropique constitue la référence par rapport à laquelle se calcule le fonctionnement de la machine réelle.

1.1.4 VANNES, FILTRES

Il existe une classe d'appareils où et Q sont nuls tous les deux : ce sont les détendeurs statiques tels que vannes, filtres... La transformation correspondante s'appelle un "laminage" isenthalpique.

Un laminage conserve l'enthalpie ( 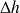= 0).

1.2.1 ECHANGEURS DE CHALEUR

Précisons tout d'abord que, dans Thermoptim, un échangeur de chaleur est constitué de deux transfos échange couplées correspondant à chacun des deux fluides, manière de faire qui présente toute une série d'avantages.

Les échangeurs de chaleur pouvant être considérés comme isobares, comme nous l'avons vu, la pression de chacun des deux fluides est la même en entrée et en sortie de la transfo échange qui le représente. Ils peuvent aussi généralement être considérés comme globalement adiabatiques, ce qui signifie que la chaleur cédée par un fluide est égale, en valeur absolue, à celle reçue par l'autre.

Une modélisation très simple d'un échangeur se limitera à cette équation, étant bien entendu que les niveaux de température dans l'échangeur doivent être tels qu'il n'y ait pas de croisement de température et que le deuxième principe soit toujours vérifié. Il faut en particulier être très vigilant lorsque l'un des fluides change d'état. Dans ce cas il est préférable de décomposer l'échangeur en sous-échangeurs connectés entre eux, les modules élémentaires étant monophasiques, sauf pour les évaporateurs et condenseurs.

Une modélisation plus poussée demande l'introduction des notions d'efficacité ou de Différence de Température Moyenne Logarithmique (DTML), relativement difficiles à bien comprendre. Elle ne sera effectuée que lors de l'étape de consolidation des connaissances (cf. troisième partie).

1.2.2 CHAMBRES DE COMBUSTION, CHAUDIERES

Même s'ils ne sont pas très compliqués, les calculs de combustion deviennent rapidement laborieux. Ce qu'il importe de bien faire comprendre aux élèves, c'est qu'ils sont basés sur la conservation des espèces et sur celle de l'enthalpie, et que la température de fin de combustion dépend de la quantité de gaz qui ne participent pas à la réaction, et notamment des inertes.

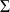
Les parois étant fixes, il n'y a pas de travail échangé avec l'extérieur ( = 0), et le bilan enthalpique devrait s'écrire 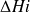= Q, la sommation étant effectuée sur toutes les espèces présentes, supposées être des gaz idéaux. Une première difficulté existe ici, car cette équation suppose que le calcul de l'énergie interne des gaz présents dans la chambre soit fait en tenant compte de l'avancement de la réaction de combustion, c'est-à-dire en considérant l'évolution des variables chimiques. Cependant il est très rare dans la pratique industrielle que l'on opère ainsi : l'enthalpie d'un gaz idéal est généralement définie par rapport à la référence standard de 1 bar et 298 K, pour une composition donnée.

Pour tourner cette difficulté, on a coutume, bien que cela soit formellement en contradiction avec le premier principe, de réintroduire un peu artificiellement dans les équations de bilan un terme de génération d'énergie dans le volume, qui correspond à la chaleur Qr libérée par la réaction de combustion. Cette manière de faire permet de ne pas tenir compte des variables chimiques, et donc de sensiblement simplifier le formalisme.

La chaleur libérée est ainsi égale au produit du débit de combustible par son Pouvoir Calorifique Inférieur (PCI), sauf dans le cas où l'eau contenue dans les fumées peut être entièrement condensée, auquel cas c'est le Pouvoir Calorifique Supérieur (PCS) qu'il faut considérer.

Les notions de facteur d'air, d'excès d'air et de richesse sont facilement compréhensibles, et les équations qui les lient sont très simples. Celles de dissociation, de température de figeage et de rendement de combustion sont plus complexes.

Le calculateur de combustions présenté section 3.3.2 de la première partie peut être utilisé pour faire faire des exercices pratiques aux élèves.

1.2.3 COMPRESSEURS ET TURBINES

Une approche simplifiée de la thermodynamique des compressions et des détentes, lorsqu'on dispose d'un accès à un simulateur, consiste à faire bien prendre conscience aux élèves que, pour un gaz parfait le travail de compression (de détente) est proportionnel à la température absolue à l'entrée de la machine, et qu'il est une fonction croissante du rapport de compression (de détente). Il est en effet inutile d'expliciter les expressions donnant ce travail, qui ne sont valables que pour les gaz parfaits.

Il importe en revanche d'introduire les notions de rendement isentropique et, si le temps disponible le permet, de rendement polytropique, en indiquant bien qu'elles sont empiriques, et que l'approche polytropique correspond à l'hypothèse que les irréversibilités sont uniformément réparties, le rendement isentropique élémentaire étant égal au rendement polytropique.

L'approche pédagogique que nous préconisons permet d'introduire progressivement dans la formation des élèves (et notamment des ingénieurs) les outils de modélisation qu'ils rencontreront de plus en plus dans l'exercice de leur métier, et de les amener ainsi à les utiliser en étant capable de les critiquer et d'en connaître les limites.

Lors de l'apprentissage de la discipline, il est ainsi possible de privilégier une approche qualitative des choses, un certain nombre de calculs nécessaires pour les études quantitatives étant réalisés par les outils logiciels de manière transparente pour les étudiants, c'est-à-dire sans qu'ils aient besoin, au moins dans un premier temps, de savoir comment ils opèrent.

Un tri doit alors être fait entre ce qu'il est fondamental de bien maîtriser au niveau quantitatif (comme par exemple les grandes lois de conservation des variables extensives^[4] et les approches simplifiées permettant une résolution analytique), et ce qui ne l'est pas.

Il ne s'agit pas de minimiser l'importance du calcul pour l'étudiant, mais simplement de tirer le meilleur parti des outils disponibles et éviter de reprogrammer ce qui existe déjà. À titre d'exemple, considérons les calculs permettant d'étudier la compression d'une vapeur dans un compresseur centrifuge ou à piston non refroidi. On sait que la transformation peut presque toujours être considérée comme adiabatique, les échanges de chaleur avec l'extérieur de la machine étant négligeables. Connaissant le rendement isentropique 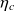  du compresseur, les conditions d'aspiration Pa, Ta et la pression de refoulement Pr, le déroulement des calculs est alors le suivant :

1. on commence par calculer l'entropie à l'aspiration s(Pa, Ta) ;

2. on cherche la température Ts correspondant à la compression adiabatique réversible, c'est-à-dire isentropique, qui est donnée par l'équation s(Pr, Ts) = s(Pa, Ta), qu'il faut inverser en Ts ;

3. on calcule ensuite l'écart d'enthalpie entre le refoulement isentropique et l'aspiration, donné par la relation 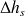= h(Pr, Ts) - h(Pa, Ta) ;

4. on en déduit l'enthalpie de fin de détente réelle hr = h(Pa, Ta) + ;

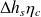5. on cherche enfin la température de refoulement Tr donnée par l'équation h(Pr, Tr) = hr qu'il faut inverser en Tr.

Alors qu'il semble fondamental que les étudiants comprennent bien (et retiennent) les cinq étapes de cette séquence de calcul et leur justification physique, il paraît moins utile qu'ils sachent par eux-mêmes calculer avec toute la précision requise les fonctions d'état enthalpie et entropie de la vapeur considérée, et a fortiori inutile qu'ils écrivent les algorithmes permettant d'inverser ces fonctions pour trouver les températures Ts et Tr. Ces calculs, qui leur prendraient beaucoup de temps, sont aussi bien sinon mieux effectués par un outil informatisé.

1.2.4 VANNES, FILTRES

La modélisation de ces composants est particulièrement simple : l'enthalpie du fluide est la même en sortie qu'en entrée.