Exemples d'études de dimensionnement technologique et de régime non nominal
Introduction
Cette page fournit quelques exemples des résultats que l'on peut obtenir lorsqu'on effectue de manière aussi rigoureuse que possible des études de dimensionnement technologique et des simulations en régime non nominal, en recalculant l'ensemble des équations reliant les composants des systèmes analysés.
Nous renvoyons à la page de présentation de cette problématique et au tome 3 de l'édition 2009 du livre Systèmes énergétiques le lecteur intéressé par de plus amples détails sur la manière de procéder.
Signalons aussi qu'il est aussi possible de bâtir des modèles moins rigoureux que ceux que nous préconisons, en se donnant des lois empiriques d'évolution de paramètres-clés comme les rendements isentropiques ou volumétriques, les pincements[1] dans les échangeurs... Cette manière de faire peut notamment présenter un intérêt didactique pour faire comprendre à des élèves les phénomènes en jeu sans pour autant entrer dans les détails des équations de couplage et des algorithmes de résolution, ou bien être parfaitement suffisante pour élaborer un modèle destiné à être inséré dans un dispositif de régulation.
Un exemple de pilote destiné à paramétrer un modèle de pompe à chaleur en fonction de la valeur de la température extérieure est proposé pour illustrer cette approche simplifiée. Ce pilote peut de plus être couplé à un contrôleur externe assurant une régulation de chauffage, dans le cadre d'un fonctionnement en réseau de Thermoptim (version 2.7 uniquement).
Nous étudierons successivement les exemples suivants :
le dimensionnement d'un échangeur air-eau ;
la détermination de la cylindrée d'un compresseur à air ;
le remplissage d'un réservoir d'air comprimé ;
le fonctionnement en régime non-nominal d'une machine de production d'eau glycolée à -10 °C.
Un lien sera enfin donné vers un autre exemple étudiant un cycle de centrale à vapeur en régime non-nominal.
Vous trouverez dans les fiches thématiques des explications sur les échangeurs de chaleur et les compresseurs volumétriques .
Exemple de dimensionnement d'échangeur
Considérons un échangeur à tubes et ailettes destiné à refroidir 0,66 kg/mn (11,7 g/s) d'air sortant d'un compresseur à 5 bars et 275 °C grâce à un débit de 1,17 kg/mn (20 g/s)d'eau froide passant dans un serpentin composé de deux tubes en parallèle. Le diamètre des tubes est de 15 mm, et leur épaisseur de 1,5 mm. L'espacement entre les ailettes est de 3 mm. On néglige dans cet exemple les résistances de paroi et d'encrassement. La puissance thermique transmise vaut 2,57 kW.
L'échangeur peut être facilement modélisé dans Thermoptim, conduisant au synoptique de la figure ci-dessous.
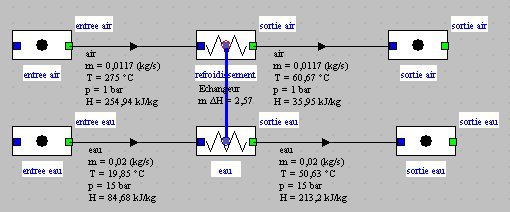
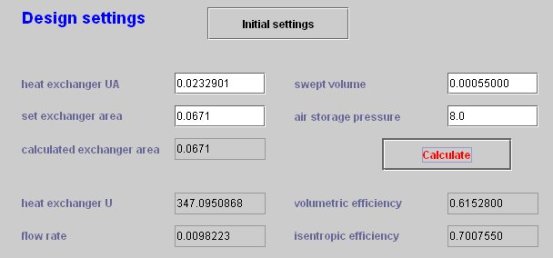
Pour dimensionner l'échangeur, on se fixe par exemple une efficacité de 0,84. L'écran de l'échangeur dans le simulateur est donné ci-dessous.
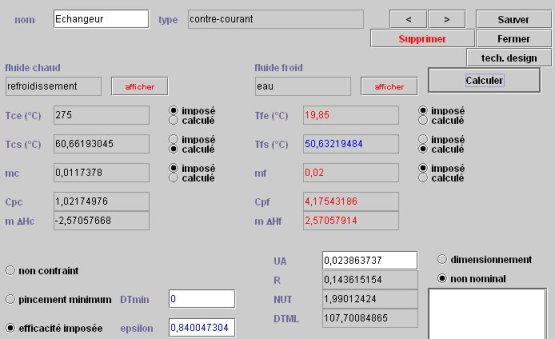
Jusqu'à présent, nous n'avons utilisé que les fonctionnalités classiques du progiciel, et le seul résultat de dimensionnement auquel nous parvenons est le produit UA du coefficient d'échange thermique par la surface de l'échangeur, sans qu'il soit possible de déterminer les valeurs de chacun de ces deux facteurs. Ici UA = 0,02386 kW/K, ou 23,86 W/K).
En utilisant les écrans de dimensionnement technologique de Thermoptim, nous allons pouvoir calculer le coefficient d'échange thermique global et en déduire la surface nécessaire pour transmettre la puissance souhaitée.
Lorsque l'on se contente de vouloir effectuer le dimensionnement technologique d'un projet qui ne met en oeuvre que des composants du noyau de Thermoptim, leurs écrans technologiques peuvent être créés automatiquement en utilisant un pilote dit générique, sans avoir besoin d'en programmer un particulier.
Une fois créé, l'accès à l'écran technologique de l'échangeur se fait en cliquant sur le bouton "techno design" situé juste au dessus du bouton "Calculer" de l'écran de l'échangeur dans le simulateur. Avant paramétrage, il se présente comme indiqué ci-dessous.
L'écran de dimensionnement technologique de l'échangeur contient dans sa partie inférieure gauche les deux zones relatives à chaque transfo "échange".
Pour le calcul des coefficients d'échange thermique et des pertes de charge, outre la surface de l'échangeur A, deux grandeurs sont toujours nécessaires : la section de passage dévolue au fluide Ac, et le diamètre hydraulique dh.
Lorsque, comme c'est le cas dans cet exemple, les coefficients d'échange thermique des fluides sont très différents, on a recours à des dispositifs divers comme des ailettes pour compenser l'écart entre leurs valeurs. On parle alors de surfaces étendues, qui peuvent être caractérisées par un facteur de surface f et un rendement d'ailette eta.
Ces quatre paramètres sont ceux qui ont été retenus pour caractériser les échanges thermiques au niveau de chaque fluide. On leur ajoute la longueur de l'échangeur pour certains calculs, notamment des pertes de charge.
Dans l'écran de dimensionnement technologique des échangeurs ci-dessus, les conventions suivantes sont adoptées :
"free flow area" représente la section de passage Ac ;
"hydr. diameter" est le diamètre hydraulique habituel dh ;
"length" est la longueur de l'échangeur ;
"surface factor" est le facteur de surface f pour les surfaces étendues ;
"fin efficiency" est le rendement d'ailettes eta ;
la résistance de paroi e/lambda est saisie dans la partie supérieure droite de l'écran, sous le bouton "Quitter". Elle permet de prendre en compte des résistances d'encrassement si on le souhaite.
Les valeurs des paramètres de dimensionnement technologique doivent être saisis pour chacun des deux fluides, ainsi que leur configuration d'écoulement choisie dans la liste proposée, ici "ext_tube" pour l'air de refroidissement, et "int_tube" pour l'eau.
C'est cette configuration d'écoulement qui précise les corrélations pour les coefficients d'échange thermique et les pertes de charge qui sont retenues pour le calcul de l'échangeur.
Il faut pour cela commencer par déterminer les diamètres hydrauliques dh et les sections de passage Ac des deux fluides.
A l'intérieur des tubes, dh est donné, et le calcul de Ac est très simple : il est égal au produit du nombre de tubes par la section unitaire.
A l'extérieur des tubes, les calculs sont un peu plus compliqués. dh est égal à 4 fois la section par le périmètre mouillé.
Quant à Ac, c'est la surface transversale offerte au passage de l'air. On a supposé que les ailettes multipliaient par 10 la surface d'échange, avec une efficacité égale à 0,8.
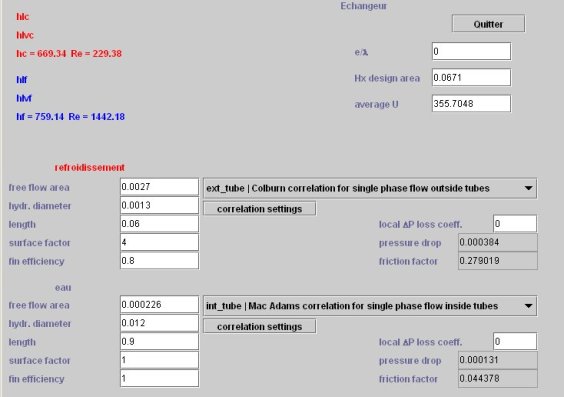
Ces valeurs doivent être entrées dans l'écran de dimensionnement technologique de l'échangeur. En reprenant le paramétrage expliqué en détail dans le fil d'Ariane sur les échangeurs de chaleur , on obtient les résultats présentés dans la figure ci-dessous

On peut alors calculer la surface A nécessaire, qui est ici égale à 0,067 m2, les coefficients d'échange valant 669 (W/m2/K) côté air et 759 (W/m2/K) côté eau, comme indiqué sur la figure, le tout conduisant à un coefficient global égal à 355,7 (W/m2/K).
L'échangeur sera donc constitué de deux tubes de 90 cm disposés en serpentin sur 3 nappes et traversant des plaques de tôle d'une surface totale de 0,31 m2 séparées les unes des autres de 3 mm.
Si l'on veut être précis, on entre cette longueur comme valeur du champ "length" côté eau, et 6 cm côté air, ce qui permet d'affiner l'estimation des pertes de charge.
Une fois l'échangeur dimensionné, son comportement en régime non-nominal peut être étudié directement à partir de son écran dans le simulateur.
Le mode de calcul "non nominal" permet en effet de calculer, par la méthode du NUT, l'échangeur en régime non nominal en considérant que ses deux températures d'entrée et ses deux débits sont imposés.
Thermoptim effectue une mise à jour des liens amont de l'échangeur à partir des transfos, puis effectue le calcul des températures aval et équilibre le bilan sur le plan enthalpique, le UA ayant la valeur entrée dans le champ de l'écran de l'échangeur. Les points et les transfos associés au module sont mis à jour en fonction des résultats. Aucune correction n'est automatiquement apportée sur UA pour tenir compte de l'évolution des coefficients d'échange en fonction des débits et des températures.
Il faut donc effectuer un nouveau calcul de l'échangeur, estimer la valeur de U qui en résulte, et modifier UA en conséquence, puis relancer le calcul, en réitérant l'opération jusqu'à stabilisation des valeurs. Nous indiquerons plus loin comment procéder pour qu'un pilote effectue ces opérations automatiquement.
Toutes les explications sur cet exemple sont fournies dans le fil d'Ariane sur les échangeurs .
Dimensionnement d'un compresseur volumétrique
Lorsque l'on cherche à dimensionner un compresseur volumétrique, la première chose est de déterminer sa cylindrée pour qu'il puisse transférer le débit de gaz désiré. Les calculs thermodynamiques conduisent alors généralement à une valeur qui ne correspond pas exactement à celles qui sont proposées par les constructeurs. La machine choisie diffère alors légèrement de celle qui était initialement désirée, de telle sorte que le débit mis en oeuvre s'écarte un peu de celui qui était recherché.
Pour représenter l'évolution du rendement volumétrique en fonction du rapport de compression, on peut généralement supposer qu'elle est linéaire, caractérisée par une ordonnée à l'origine (ou plus précisément pour un rapport de compression égal à 1), et une pente négative.
Pour illustrer le type de problème de dimensionnement que l'on rencontre, nous allons considérer un schéma qui sera utilisé dans l'exemple suivant traitant de comportement en régime non-nominal.
Il s'agit d'un compresseur volumétrique à air qui remplit un stockage d'air comprimé de volume donné à pression variable.
L'air comprimé est refroidi avant stockage grâce à un échangeur à eau du type de celui qui vient d'être présenté.
Le système peut être facilement modélisé dans Thermoptim et conduit à un schéma du type de celui de la figure ci-dessous, qui ne se distingue de celui étudié lors de l'exemple précédent que par l'ajout du compresseur.
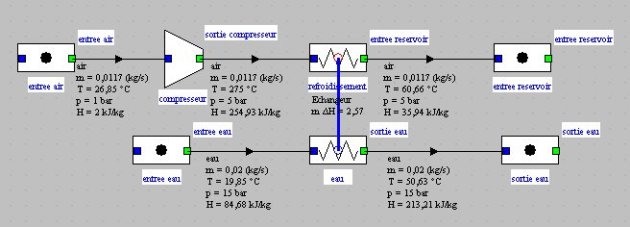
Dans cet exemple, on suppose que la vitesse de rotation du compresseur est égale à 1500 tr/mn, et on cherche quelle est la cylindrée nécessaire pour comprimer de 1 à 5 bars le débit mis en jeu dans l'exemple précédent, soit 0,01738 kg/s d'air.
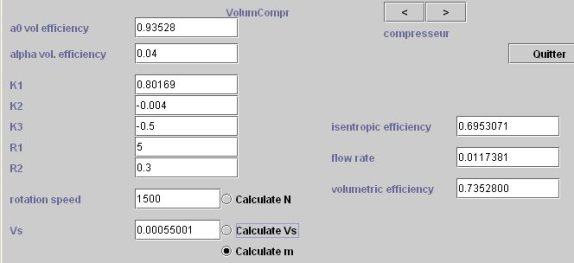
Le pilote utilisé est présenté dans la figure suivante. En cliquant sur le bouton "Initial settings", après avoir sélectionné dans le TechnoDesign du compresseur l'option "Calculate Vs" afin que Thermoptim sache que cette valeur doit être calculée, la cylindrée nécessaire est affichée dans le champ intitulé "Vs", soit 0,00055 m3, ou 0,55 l.
Une recherche dans les catalogues du constructeur montre quelle cylindrée disponible est la plus proche.
Pour modifier le modèle, l'utilisateur peut alors avoir à remplacer la cylindrée calculée par cette nouvelle valeur.
Le recalcul conduit alors à un débit mis en oeuvre qui peut être légèrement différent de celui qui avait été envisagé.
Etude d'un compresseur refroidi servant à charger un réservoir d'air comprimé
Pour illustrer la capacité qu'a Thermoptim d'effectuer des calculs en régime non-nominal, nous allons maintenant étudier le comportement du compresseur volumétrique à air que nous venons de présenter, lorsqu'on l'utilise pour remplir un stockage d'air comprimé de volume donné à pression variable.
Le modèle retenu pour le compresseur prend en compte ses rendements volumétrique et isentropique comme fonctions du rapport de compression. Le premier est donné comme nous l'avons vu par une simple relation affine, et le second a l'allure de la figure ci-dessous (l'équation que nous avons retenue est toutefois à cinq paramètres).

L' écran de dimensionnement technologique du compresseur est donné ci-dessous. Celui de l'échangeur est similaire au précédent.
Rôle du pilote
Pour obtenir les résultats recherchés, il faut construire un pilote, dont l'écran a été présenté plus haut. Il permet de faire varier le rapport de compression pour obtenir les évolutions des principales grandeurs lorsque la pression du réservoir varie, en opérant comme suit :
mise à jour de la pression de sortie du compresseur
calcul du rendement volumétrique du compresseur
calcul du rendement isentropique du compresseur
recalcul du compresseur et de la transfo aval
mise à jour des entrées et sorties de l'échangeur
détermination de U puis mise à jour de UA et recalcul de l'échangeur en mode non-nominal (en plusieurs itérations étant donné que U dépend des températures moyennes des fluides, et donc de celles de sortie)
mise à jour du simulateur et des affichages
On notera que dans cet exemple le comportement du compresseur ne dépend pas, une fois le rapport de compression défini, de celui de l'échangeur situé en aval : il n'y a pas de couplage systémique, du moins pour un point de fonctionnement donné.
La conception du pilote en est facilitée : il n'y a pas à résoudre de système d'équations non linéaires de couplage, comme ce sera le cas dans le prochain exemple.
Une fois le pilote réalisé, il est très facile de faire varier le rapport de compression pour obtenir les évolutions des principales grandeurs lorsque la pression du réservoir varie.
Elles peuvent être exploitées avec la macro Excel de post-traitemen t des fichiers de simulation de Thermoptim présentée au tome 1 du manuel de référence. Il suffit pour cela de sauvegarder le fichier de projet sous un nom différent après chaque simulation, puis de charger ces fichiers dans la macro et d'en extraire les valeurs intéressantes.
La figure ci-dessous montre, en fonction de la pression du stockage, les évolutions du rendement isentropique du compresseur, du travail consommé, du débit d'air aspiré, de la température de l'air entrant dans le réservoir, de la charge de l'échangeur et de UA.

Il serait possible d'exploiter ce modèle de plusieurs manières, comme calculer le travail nécessaire pour compenser les pertes de charge...
L'ensemble des fichiers correspondant à cet exemple est donné dans la modélothèque.
Utilisation du modèle pour simuler le remplissage d'un stockage d'air comprimé
Les résultats de la figure ci-dessus peuvent être utilisés pour simuler le remplissage d'un stockage d'air comprimé. Thermoptim ne fournissant de résultats que pour un régime stabilisé, le plus simple est de développer un second modèle, résolu sous Excel.
Ses équations sont les suivantes :
la masse M d'air contenue dans le stockage est égale à la masse initiale plus l'intégrale du débit ;
l'énergie interne U est égale à l'énergie interne initiale plus l'intégrale du produit du débit par l'enthalpie de l'air sortant du refroidisseur, moins l'intégrale des pertes par convection avec l'air ambiant ;
la température du stockage est déduite de son énergie interne ;
la pression se calcule alors par la loi des gaz idéaux.
Pour connaître le débit, le travail de compression et la température de l'air en entrée de stockage, il suffit de faire des régressions polynomiales à partir des simulations effectuées précédemment avec Thermoptim. Les équations obtenues sont, en fonction du rapport de compression r :

L'allure des résultats est donnée figure ci-dessous, pour un stockage d'un demi m3 (diamètre 80 cm, longueur 1 m), alimenté par un compresseur de cylindrée Vs = 0,525 l. La pression et la température dans le stockage, sa masse et le travail à fournir au compresseur sont affichés.

L'ensemble des fichiers correspondant à cet exemple est donné dans la modélothèque.
Comportement en régime non-nominal d'une machine frigorifique
Nous allons maintenant étudier un problème beaucoup plus complexe, celui de l'adaptation d'une machine frigorifique à la variation de la température extérieure ou de la vitesse de rotation de son compresseur.
Jusqu'ici, nous n'avons abordé que des problèmes relativement simples, qui ne mettaient pas en jeu des équations de couplage systémique entre les différents composants. Dans cet exemple, ce n'est plus le cas :
tout d'abord, les niveaux de pression sont imposés par les équilibres thermiques des deux échangeurs à changement de phase, l'évaporateur et le condenseur, qui fixent les températures de saturation ;
quant au compresseur, il impose le débit volumique de frigorigène (en fonction de sa vitesse de rotation et du rapport de compression qui déterminent son rendement volumétrique), et donc le débit massique (fonction du volume massique de frigorigène à l'aspiration).
Les paramètres principaux de la machine frigorifique, à savoir les niveaux de pression et le débit, sont ainsi imposés par plusieurs composants fortement couplés dont le calcul ne peut plus être fait indépendamment.
De surcroît, nous imposerons deux contraintes complémentaires :
nous prendrons en compte les pertes de charge dans les échangeurs ;
le sous-refroidissement sera déterminé en assurant la conservation de la masse globale de frigorigène contenu dans la machine.
Paramétrage du cycle
Supposons que l'on veuille dimensionner un cycle de réfrigération simple (figure ci-dessous) pour qu'il fournisse une puissance frigorifique de 130 kW pour une température extérieure de 30 °C, la température de l'eau glycolée étant égale à -10 °C en entrée de l'évaporateur. Pour ce cycle, le fluide froid est du propylène glycol à 40 % en volume, disponible dans les corps externes. La température d'évaporation doit bien évidemment être inférieure à celle de l'eau glycolée. Nous avons retenu environ –21,6 °C, c'est-à-dire une pression de 1,24 bars pour du R134a.
On suppose que le rendement isentropique du compresseur vaut environ 0,8 au point nominal. Pour simplifier un peu le modèle on fait l'hypothèse que la valeur de la surchauffe à l'évaporation reste constante (5 K). Celle du sous-refroidissement à la condensation est en revanche déterminée sur la base de la masse globale de frigorigène, qui reste constante dans la machine.
La surchauffe à l'évaporation DTsurch vaut 5 K, ce qui pour un débit de réfrigérant de 0,955 kg/s fixe la puissance frigorifique à environ 131 kW. Avec un débit d'eau glycolée de 15 kg/s, cela conduit à un refroidissement de 2,42 °C. Pour le condenseur, la température de l'air vaut 30 °C, et son débit 25 kg/s. La température de condensation est estimée à 42 °C, ce qui, avec un sous-refroidissement initial DTssrefr de 5 K, correspond à une pression de condensation d'environ 10,9 bars. Le COP de la machine vaut dans ces conditions 2,24.

La prise en compte des pertes de charge du réfrigérant demande quelques précautions pour éviter des difficultés de calcul dans les phases de condensation et d'évaporation. Nous avons choisi de les affecter uniquement aux points dont l'état[2] est monophasique : en totalité en aval de l'évaporateur, et pour moitié en amont et en aval du condenseur.
Les pertes de charge sur l'air et l'eau glycolée sont calculées dans les écrans technologiques des échangeurs, puis affectées comme surpression à réaliser en amont de l'échangeur. Les ventilateurs et la pompe à eau glycolée sont ici modélisés par des transfos compression classiques, sans prise en compte de leurs caractéristiques détaillées. Il serait possible de le faire, mais au prix d'une complexité accrue qui n'apparaît pas vraiment justifiée.
Le dimensionnement se fait en deux étapes distinctes, la première correspond au paramétrage classique du cycle dans Thermoptim, tandis que la seconde est effectuée à partir des écrans technologiques. Précisons, et ceci est très important, que la deuxième étape ne peut être effectuée que lorsque la première a été menée à son terme et a permis d'obtenir un modèle parfaitement cohérent. Si ce n'est pas le cas, le dimensionnement technologique effectué au cours de la seconde étape risque d'être aberrant et d'entraîner de grandes difficultés de convergence.
Nous ne détaillerons pas ici, pour simplifier les choses, la manière de construire le modèle Thermoptim du cycle correspondant à la première étape. S'il n'existait pas, il faudrait d'abord le faire, puis la méthode serait la même. Ce cycle de réfrigération est semblable à ceux qui ont été présentés dans les guides de prise en mains du progiciel, la différence principale étant que le condenseur est modélisé par un seul échangeur multizone, la désurchauffe n'étant pas dissociée dans l'éditeur de schémas de la condensation proprement dite.
Ecran du pilote
La partie supérieure de l'écran du pilote est donnée figure ci-dessous. Elle permet de modifier d'une part les surfaces des échangeurs, et d'autre part la longueur de la ligne liquide, la température d'air, la vitesse de rotation ou la cylindrée, et possède des options de guidage de l'algorithme qui seront précisées plus loin.
Par défaut, c'est la vitesse de rotation qui est calculée, pour la valeur de la cylindrée entrée à l'écran. Si vous choisissez l'option "Calculate Vs", c'est la cylindrée qui est calculée, pour la valeur de la vitesse de rotation saisie.
Commencez par cliquer sur "Initial settings" pour instancier les TechnoDesign et effectuer un premier dimensionnement technologique, en l'occurrence calculer la vitesse de rotation ou la cylindrée du compresseur ainsi que les surfaces des deux échangeurs correspondant au paramétrage du fichier de projet, sur la base des valeurs par défaut des paramètres des TechnoDesign.

Paramétrage des écrans technologiques
Les écrans technologiques ayant été créés, vous pouvez passer à leur paramétrage puis à leur dimensionnement. Cette étape doit être faite avec soin, car elle suppose d'effectuer toute une série de choix quant aux configurations internes, aux dimensions géométriques...
Pour accéder aux écrans technologiques, faites-le à partir des tables de l'écran général depuis le simulateur (Ctrl T), ou bien à partir des boutons "tech. design" des écrans classiques des composants.
On considère que l'évaporateur est du type tubes et calandre et qu'il a côté eau une section de passage du fluide de 8 dm2 et un diamètre hydraulique de 1 cm, et côté réfrigérant une section de passage de 2 dm2 et un diamètre hydraulique de 1 cm, pour une longueur de tubes de 3 m. Choisissez le type de configuration ("evap Gungor Winterton" pour évaporation à l'intérieur des tubes pour la partie "évaporateur" (le frigorigène), et "ext tube Colburn correlation" pour l'eau glycolée, et paramétrez l'écran comme indiqué figure ci-dessous.

Le condenseur est du type batterie à ailettes. Côté air il a une section de passage du fluide de 1 m2 et un diamètre hydraulique de 1 cm avec un facteur de surfaces étendues de 20, sur une longueur de 15 cm (épaisseur de l'aérocondenseur), et côté réfrigérant une section de passage de 0,5 dm2 et un diamètre hydraulique de 2 cm, pour une longueur de tubes de 3 m. Choisissez le type de configuration ("cond Shah correlation" pour la condensation à l'intérieur des tubes pour la partie "condenseur" (le frigorigène), et "air coil Morizot correlation" pour l'air, et paramétrez l'écran comme indiqué figure ci-dessous.

Pour le compresseur (figure ci-dessous), il faut fournir d'une part la cylindrée Vs, et d'autre part les valeurs des paramètres qui interviennent dans les équations des rendements volumétrique et isentropique.

Pour réaliser le dimensionnement une fois les écrans technologiques renseignés, recliquez sur le bouton "Initial settings" de l'écran du pilote.
Les résultats sont affichés dans les écrans technologiques : surfaces d'échanges de 25 m2 pour l'évaporateur et le condenseur ; vitesse de rotation de 1500 tr/mn et cylindrée d'environ 0,01 m3 pour le compresseur.
Divers résultats de calcul sont affichés sur les écrans technologiques, comme, pour les échangeurs, les pertes de charge et les valeurs du nombre de Reynolds Re et des coefficients d'échange locaux.
Résolution du système d'équations de la machine frigorifique en non-nominal
Dans toute étude de comportement en régime non-nominal, il faut bien identifier quelles sont les variables indépendantes du système considéré, en les distinguant des variables liées qui s'en déduisent. Dans cet exemple, il s'agit du quadruplet (débit de réfrigérant, température d'évaporation, température de condensation, sous-refroidissement), les variables liées étant les pressions du fluide et les puissances thermiques et mécaniques mises en jeu.
A ces quatre variables "naturelles" , il faut ajouter les deux variables intermédiaires UAevap et UAcond qui permettent d'assurer le calcul des échangeurs, le critère de convergence étant que leurs surfaces restent égales à celles de dimensionnement. La recherche de ce sextuplet correspond à celle de la solution d'un jeu d'équations non linéaires relativement complexe.
La solution que nous avons retenue consiste à programmer un pilote externe qui assure la résolution de ce système d'équations et met à jour Thermoptim une fois la solution trouvée.
Nous utilisons la méthode de Levendberg-Marquardt correspondant aux algorithmes mis au point en Fortran sous le nom de minPack 1, et traduits sous Java. Cette méthode combine l'algorithme de Gauss-Newton et la méthode de descente de gradient. Son intérêt principal est d'être très robuste et de ne nécessiter comme initialisation qu'une solution approchée.
Elle demande d'exprimer chaque équation sous forme d'une fonction renvoyant l'écart, appelé résidu, entre la valeur à atteindre et la valeur calculée.
Le guidage de l'algorithme se fait en pratique en jouant sur deux critères de précision, l'un portant sur la somme des résidus, et l'autre sur la précision du calcul des dérivées partielles, estimées par différences finies. N'oublions pas que nous cherchons à résoudre un système de six équations non linéaires à six inconnues, ce qui peut se révéler numériquement difficile. A l'usage, il est apparu intéressant de proposer plusieurs options de calcul.
Tout d'abord, l'option "reinitialize" offre la possibilité de réinitialiser les valeurs des températures d'évaporation et de condensation en fonction de celles de l'eau glycolée et de l'air ambiant, pour éviter tout croisement de température dans les échangeurs.
Ensuite, deux options exclusives sont proposées : soit exécuter l'algorithme en une seule étape, pour des valeurs intermédiaires de précision des critères de convergence ("one step algorithm"), soit l'exécuter en deux étapes, la première permettant une convergence grossière, et la seconde plus précise ("two steps algorithm").
Selon les cas, l'utilisateur peut opter pour l'une ou l'autre, en fonction des difficultés numériques rencontrées. Un indicateur de précision, correspondant à la norme L2 des résidus, est affiché dans la partie résultat de l'écran du pilote (figure ci-dessous).
S'il lance les calculs depuis l'écran général des écrans technologiques, l'utilisateur peut de surcroît s'il le désire interrompre les calculs proprement en cliquant sur le bouton "Stop", ce qui lui permet de changer d'option. Attention toutefois, car cette manière d'opérer peut conduire à des erreurs.
Résultats de simulation

L'écran complet du pilote est donné ci-dessus. Il permet de modifier d'une part les surfaces des échangeurs et la longueur de la ligne liquide, et d'autre part la température d'air, la cylindrée ou la vitesse de rotation.
Entrez la température d'air ou la vitesse de rotation que vous souhaitez modifier, et, soit cliquez sur "Calculate", soit ouvrez l'écran des TechnoDesign depuis le simulateur, puis cliquez sur "Calculer le pilote". Cette deuxième manière de faire est préférable, car elle permet de suivre la convergence tout en gardant la main sur Thermoptim, pour afficher des valeurs intermédiaires ou modifier les calculs du pilote. Les résultats sont affichés à l'écran une fois la convergence obtenue.
Si les valeurs que vous entrez sont très différentes de celles de dimensionnement, des erreurs de calcul de Thermoptim peuvent être générées, avec messages. Si nécessaire, choisissez une valeur de recalcul plus proche de la valeur initiale.
Les figures ci-dessous montrent les résultats de simulation obtenus lorsque l'on fait varier la température de l'air de refroidissement, pour le paramétrage des écrans technologiques retenu précédemment, la vitesse de rotation étant égale à 1 500 tr/mn. Elles montrent bien la non-linéarité du comportement de la machine.
On notera en particulier que les coefficients d'échange thermique varient significativement, ce qui justifie pleinement qu'on ne les considère pas constants comme beaucoup d'auteurs en font l'hypothèse.



L'influence de la vitesse de rotation est donnée dans les figures ci-dessous, pour une température extérieure de 30 °C.



Dans cet exemple, nous n'avons fait varier que deux variables, mais il serait très simple d'étudier l'influence des débits d'air et d'eau glycolée, ou de la température de cette dernière, soit en modifiant leurs valeurs dans les écrans du simulateur avant recalcul avec ce pilote, soit en le modifiant pour que ces valeurs apparaissent dans l'écran de pilotage et soient ensuite automatiquement mises à jour.
L'ensemble des fichiers correspondant à cet exemple est donné dans la modélothèque.
Un exemple analogue a été bâti pour expliquer comment créer un pilote pour l'étude en régime de fonctionnement non-nominal d'un cycle de centrale à vapeur. Il est lui aussi disponible dans la modélothèque. Etant donné qu'il s'apparente beaucoup à l'exemple que nous venons de présenter, nous ne le développons pas ici.
Précisons que des approfondissements ont été réalisés en 2021 sur les corrélations relatives aux pertes de charge et aux coefficients d'échange thermique utilisées depuis 2009, afin de tenir compte des nombreux résultats publiés au cours des douze dernières années.
Certaines approximations qui avaient été initialement faites pour réduire les temps de calcul ont à cette occasion été remises en cause, les processeurs actuels étant beaucoup plus rapides qu'à l'époque.
Quelques erreurs ont aussi été détectées et corrigées, et certains modèles ont été complétés.
Il en résulte que les résultats fournis par les versions de fin 2021 présentent quelques différences avec ceux de 2009 présentés ci-dessus. Elles portent essentiellement sur les valeurs des surfaces calculées, les allures des évolutions en régime non nominal restant semblables.
Les principaux écarts constatés sont expliqués dans les pages de la modélothèque fournissant les fichiers de ces modèles.
Un document (en anglais) expliquant comment utiliser en pratique le pilote construit pour le calcul en régime non-nominal de la machine de réfrigération peut être téléchargé à partir du lien ci-dessous, ainsi que les fichiers de résultats et les feuilles de calcul Excel pour cette machine de réfrigération et pour la centrale à vapeur simplifiée mentionnée ci-dessus.
Exemple de dimensionnement d'un échangeur
Explorations dirigées
Ces trois explorations dirigées vous permettront de vous initier à ces exemples.
Cette exploration montre comment la surface d'un échangeur de chaleur peut être déterminée et comment son comportement en régime non-nominal peut être calculé.
L'exploration (OPT-1) a montré comment peut être mise en application la méthode du pincement pour optimiser un réseau de chaleur.
Cette exploration, qui la complète, porte sur le dimensionnement et l'étude en régime non-nominal d'un compresseur à piston servant à alimenter un réservoir de stockage d'air comprimé.
Dans cette exploration nous détaillons le calcul et le dimensionnement d'un compresseur à piston servant à alimenter un réservoir de stockage d'air comprimé
Remarque
Comme précisé plus haut, les versions de Thermoptim qui permettent d'effectuer les études de dimensionnement technologique et de fonctionnement en régime non-nominal sont les versions 2.7 et 2.8.


