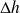11 Représentation graphique de cycles dans le diagramme (h, ln(P))
Nous allons maintenant expliquer comment tracer dans le diagramme (h, ln(P)) les cycles de la centrale à vapeur, de la turbine à gaz et de la machine de réfrigération. Nous supposerons dans un premier temps que les compressions et détentes sont parfaites, c'est-à-dire suivent des adiabatiques réversibles. Ensuite, nous tiendrons compte des irréversibilités grâce aux rendements isentropiques de compression et de détente.
Sur le plan pratique, les activités proposées dans cette section devraient être faites à la main, les élèves disposant de diagrammes sur papier. Ceux-ci peuvent être soit imprimés directement à partir de Thermoptim, mais leur précision n'est pas très grande, soit obtenus dans le commerce ou dans des ouvrages spécialisés.
Nous n'avons pas encore précisé les données numériques relatives à ces cycles. Nous allons le faire maintenant, en choisissant des valeurs facilement représentables, et les construire pas à pas dans ce diagramme.
Nous supposerons que la turbine à gaz fonctionne avec de l'air parce que l'estimation des propriétés thermodynamiques des produits de combustion demande des précautions particulières.
11.1 Centrale à vapeur
Au point 1 en sortie de condenseur (figure ci-dessous), l'eau est à l'état liquide, à une température d'environ 27 °C, sous une faible pression (0,0356 bar). Sur la figure, le point est facile à repérer, à l'intersection de l'isotherme T = 27 °C et de la courbe de saturation.

La pompe la comprime à environ 128 bar, ce qui représente un rapport de compression considérable (de l'ordre de 3600).
La température T restant sensiblement constante pendant la compression (1- 2) le point 2 se situe à l'intersection de l'isotherme T = 27 °C et de l'isobare P = 128 bar (horizontale d'ordonnée 128 bar).
L'eau sous pression est ensuite portée à haute température dans la chaudière, l'échauffement comportant les trois étapes suivantes :
chauffage du liquide de près de 27 °C à environ 330 °C, juste au-dessus de l'isotherme T = 327 °C, température de début d'ébullition à 128 bar : évolution (2-3a). Le point 3a se trouve sur la courbe de vaporisation cette même isobare ;
vaporisation à température constante 330 °C : évolution (3a-3b). La vaporisation s'effectuant à pression et température constantes, elle se traduit sur le diagramme par un segment horizontal 3a-3b. Le point 3b se trouve donc sur la branche descendante de la courbe de vaporisation, ou courbe de rosée, à son intersection avec la droite horizontale de pression 128 bar ;
surchauffe de 330 °C à 447 °C : évolution (3b-3). Le point 3 est encore par hypothèse à la même pression, mais à une température T3 de 447 °C. Il se trouve donc à l'intersection de l'horizontale P = 128 bar et de l'isotherme T = 447 °C (représentée uniquement partiellement sur la figure).
Le point 3 se trouve par ailleurs sur une courbe inclinée à concavité tournée vers le bas correspondant à une adiabatique réversible.
L'évolution (3-4) est une détente adiabatique réversible de 128 bar à 0,0356 bar. Le point étant dans la zone mixte, cette dernière est confondue avec l'isotherme T = 27 °C. Le point 4 est donc à l'intersection de la courbe inclinée à concavité tournée vers le bas et de cette isotherme. Son titre x est compris entre 0,7 et 0,8. Par interpolation linéaire on peut l'estimer égal à 0,72.
Comme on le voit sur cet exemple, la représentation du cycle dans le diagramme (h, ln(P)) est très parlante sur le plan physique : les échanges de chaleur, quasiment isobares, correspondent aux segments horizontaux, et les compressions et les détentes sont des adiabatiques réversibles, d'autant moins pentues que l'on s'écarte de la zone liquide.
Les enthalpies des points peuvent être directement lues en projetant ces différents points sur l'axe des abscisses. Le tableau ci-dessous fournit ces valeurs.
point | débit (kg/s) | h (kJ/kg) |
1 | 1 | 113 |
2 | 1 | 126 |
3a | 1 | 1524 |
3b | 1 | 2672 |
3 | 1 | 3189 |
4 | 1 | 1870 |
Les énergies mises en jeu dans chacune des transformations se déduisent par simple différence des enthalpies des points et conduisent au tableau ci-dessous. Notons que la lecture dans ce diagramme du travail de compression est très imprécise et qu'il est préférable de l'estimer à partir de l'intégration de
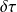 = v dP, très facile à effectuer, v étant constant. Il vaut donc
= v dP, très facile à effectuer, v étant constant. Il vaut donc
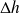 = v
= v
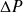 , P étant exprimé en Pa.
, P étant exprimé en Pa.
transformation |
| Q (kW) |
|
(1-2) | 13 | 13 | |
(2-3a) | 1398 | 1398 | |
(3a-3b) | 1148 | 1148 | |
(3b-3) | 517 | 517 | |
(3-4) | -1319 | -1319 | |
(4-1) | -1757 | -1757 | |
cycle | -1306 | 1306 |
Le rendement est ici le rapport du travail mécanique produit à la chaleur fournie par la chaudière. Il est égal à 42,6 %.
Prise en compte des écarts par rapport aux évolutions de référence
Dans la réalité, la turbine n'est pas parfaite, et la détente suit une adiabatique non réversible. Comme nous l'avons expliqué, la transformation réelle est caractérisée par un rendement isentropique
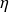 , défini dans le cas d'une turbine comme le rapport du travail réel au travail de la détente réversible.
, défini dans le cas d'une turbine comme le rapport du travail réel au travail de la détente réversible.
Pour trouver le point 4' réel, on détermine la valeur du travail
 s mis en œuvre dans la machine parfaite, on la multiplie par
s mis en œuvre dans la machine parfaite, on la multiplie par
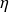 , ce qui donne la valeur du travail réel
, ce qui donne la valeur du travail réel
 .
.
Comme
 = h3 – h4', l'enthalpie du point 4' est égale à celle du point 3 moins
= h3 – h4', l'enthalpie du point 4' est égale à celle du point 3 moins
 .
.
Dans le cas présent, en prenant
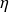 = 0,9, on a :
= 0,9, on a :
 s = h3 – h4 = 1319 kJ/kg
s = h3 – h4 = 1319 kJ/kg
 =
=
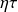 s = 0,9 . 1319 = 1187
s = 0,9 . 1319 = 1187
h4' = 3199 – 1187 = 2002 kJ/kg
Le point 4', qui est toujours dans la zone d'équilibre liquide-vapeur, se situe donc sur l'isobare P = 0,0356 bar, ou ce qui revient au même sur l'isotherme T = 27 °C, à l'abscisse h = 2002 kJ/kg/K, le titre en vapeur valant 0,775. La figure ci-dessous montre la nouvelle allure du cycle (le cycle précédent est représenté en tiretés).
L'augmentation du titre en fin de détente est favorable d'une part à la prolongation de la durée de vie des aubages de la turbine, pour qui les gouttelettes de liquide constituent des abrasifs redoutables, et d'autre part au rendement isentropique, qui chute lorsque l'humidité augmente.
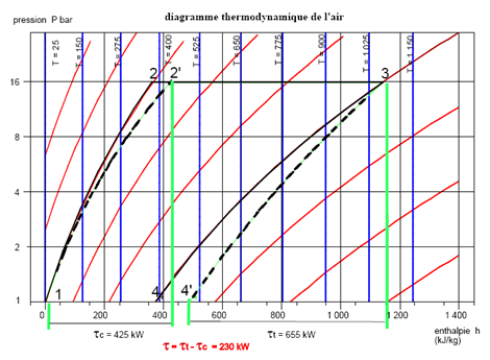
11.2 Turbine à gaz
La turbine à gaz aspire 1 kg/s d'air à 25 °C et 1 bar et le comprime à 16 bar dans un compresseur parfait. Cet air est porté à la température de 1065 °C dans la chambre de combustion, puis est détendu dans une turbine parfaite.
Dans le diagramme (h, ln(P)) de la figure ci-dessous, le point 1 se trouve sur l'axe des abscisses, à l'intersection avec l'isotherme T = 25 °C (h = 0). La compression parfaite le long de l'adiabatique réversible conduit au point 2, intersection de cette courbe et de l'horizontale P = 16 bar. L'enthalpie se lit sur l'axe des abscisses et vaut h = 360 kJ/kg.

L'échauffement dans la chambre de combustion conduit au point 3, à l'intersection de l'isobare P = 16 bar et de l'isotherme T = 1065 °C (h = 1140 kJ/kg).
L'évolution (3-4) est une détente adiabatique réversible de 16 bar à 1 bar. Le point 4 est donc à l'intersection de l'adiabatique réversible et de l'axe des abscisses (h = 375 kJ/kg).
Ce diagramme permet de bien comprendre pourquoi la turbine à gaz peut fonctionner : plus la température augmente, moins les pentes des adiabatiques réversibles sont fortes, et donc plus l'énergie mise en jeu dans la transformation est importante, pour un rapport de pression donné: la variation d'enthalpie (3-4) croît beaucoup plus vite que le travail de compression (1-2). On a donc intérêt à travailler à P et T aussi grands que possible.
Pour le paramétrage retenu, le travail de compression
 c à 1 bar et 25 °C est plus de deux fois plus faible que le travail de détente
c à 1 bar et 25 °C est plus de deux fois plus faible que le travail de détente
 d à 16 bar et 1065 °C.
d à 16 bar et 1065 °C.
On comprend aussi pourquoi les performances de la machine dépendent beaucoup de la température de l'air ambiant : plus elle est basse, plus la pente de l'adiabatique réversible est forte et donc plus le travail de compression est faible.
L'énergie utile est la valeur absolue de la somme algébrique du travail fourni au compresseur et produit par la turbine (410 kW), et l'énergie payante la chaleur fournie par la chambre de combustion (h3 – h2 = 780 kW). Le rendement s'en déduit.
point | débit (kg/s) | h (kJ/kg) |
1 | 1 | 0 |
2 | 1 | 360 |
3 | 1 | 1140 |
4 | 1 | 370 |
Les énergies mises en jeu dans chacune des transformations se déduisent par simple différence des enthalpies des points et conduisent au tableau ci-dessous.
transformation |
| Q (kW) |
|
(1-2) | 360 | 360 | |
(2-3) | 780 | 780 | |
(3-4) | - 770 | -770 | |
échappement | |||
cycle | - 410 | 780 |
Le rendement est ici le rapport du travail mécanique produit à la chaleur fournie à la chambre de combustion. Il est égal à 52,6 %.
Prise en compte des écarts par rapport aux évolutions de référence
Dans la réalité, le compresseur et la turbine ne sont pas parfaits, et la compression et la détente suivent des adiabatiques non réversibles. Comme nous l'avons expliqué précédemment, la transformation réelle est caractérisée par un rendement isentropique
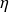 , défini défini dans le cas du compresseur comme le rapport du travail de la compression réversible au travail réel, et dans le cas d'une turbine comme le rapport du travail réel au travail de la détente réversible.
, défini défini dans le cas du compresseur comme le rapport du travail de la compression réversible au travail réel, et dans le cas d'une turbine comme le rapport du travail réel au travail de la détente réversible.
Pour trouver le point 2' réel, on détermine donc la valeur du travail
 s mis en œuvre dans le compresseur parfait et on la divise par
s mis en œuvre dans le compresseur parfait et on la divise par
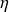 , ce qui donne la valeur du travail réel
, ce qui donne la valeur du travail réel
 .
.
Comme
 = h2' – h1, l'enthalpie du point 2' est égale à celle du point 1 plus
= h2' – h1, l'enthalpie du point 2' est égale à celle du point 1 plus
 .
.
Dans le cas présent, en prenant
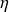 = 0,85, on a :
= 0,85, on a :
 s = h2 – h1 = 360 kJ/kg
s = h2 – h1 = 360 kJ/kg
 =
=
 s/
s/
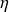 = 360/0,85 = 424
= 360/0,85 = 424
h2' = 424 kJ/kg
Pour trouver le point 4' réel, on détermine la valeur du travail
 s mis en œuvre dans la machine parfaite, on la multiplie par
s mis en œuvre dans la machine parfaite, on la multiplie par
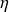 , ce qui donne la valeur du travail réel
, ce qui donne la valeur du travail réel
 .
.
Comme
 = h3 – h4', l'enthalpie du point 4' est égale à celle du point 3 moins
= h3 – h4', l'enthalpie du point 4' est égale à celle du point 3 moins
 .
.
Dans le cas présent, en prenant
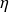 = 0,85, on a :
= 0,85, on a :
 s = h3 – h4 = 765 kJ/kg
s = h3 – h4 = 765 kJ/kg
 =
=
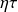 s = 0,85 . 765= 654
s = 0,85 . 765= 654
h4' = 1140– 654= 486 kJ/kg
La figure ci-dessous montre la nouvelle allure du cycle (avec des tirets, le cycle précédent étant représenté en trait continu).
Le rendement chute considérablement (il vaut 32 % au lieu de 52,6 %), du fait que le travail net, égal à la différence en valeur absolue entre le travail de détente et celui de compression, est fortement diminué. Le travail de compression a augmenté de 65 kW, mais surtout le travail de détente a chuté de 115 kW, la perte totale étant de 180 kW.
11.3 Machine de réfrigération
Le cycle de réfrigération par compression de R134a (figure ci-dessous) fonctionne entre une pression d'évaporation de 1,78 bar et une pression de condenseur de 12 bar.
Au point 1, en sortie d'évaporateur, le fluide est entièrement vaporisé, et donc à l'intersection de la courbe de saturation et de l'isobare P = 1,78 bar, ou, ce qui revient au même, de l'isotherme T = - 13 °C.
Il est ensuite comprimé jusqu'à 12 bar en suivant une compression adiabatique réversible. Le point 1 se situant à peu près au tiers de la distance qui sépare deux adiabatiques réversibles, on peut par interpolation linéaire, déterminer le point 2 qui se situe sur l'isobare P = 12 bar, entre ces deux courbes.
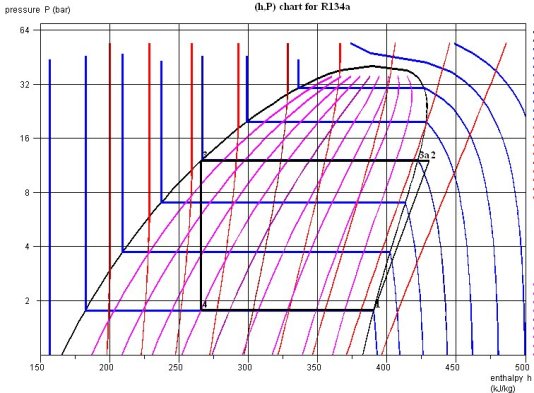
Le refroidissement du fluide dans le condenseur par échange avec l'air extérieur comporte deux étapes : une désurchauffe (2-3a) dans la zone vapeur suivie d'une condensation selon le segment de droite horizontal (3a-3). Les points 3a et 3 se situent à l'intersection de la courbe de saturation et de l'isobare P = 12 bar, ou, ce qui revient au même, de l'isotherme T = 47 °C. Le point 3a est situé sur la droite, à la limite de la zone vapeur, et le point 3 à gauche, à la limite de la zone liquide.
La détente sans travail, et donc isenthalpique, correspond au segment vertical (3-4), le point 4 étant situé sur l'isobare P = 1,78 bar, ou, ce qui revient au même, l'isotherme T = - 13 °C, à l'abscisse h = h3. Son titre se lit directement sur l'iso-titre correspondante : il vaut x = 0,4.
Les énergies mises en jeu peuvent être facilement déterminées en projetant ces différents points sur l'axe des abscisses. Le tableau ci-dessous fournit ces valeurs.
point | débit (kg/s) | h (kJ/kg) |
1 | 1 | 391 |
2 | 1 | 430 |
3a | 1 | 422 |
3 | 1 | 266 |
4 | 1 | 266 |
Les énergies mises en jeu dans chacune des transformations se déduisent par simple différence des enthalpies des points et conduisent au tableau ci-dessous.
transformation |
| Q (kW) |
|
(1-2) | 40 | 40 | |
(2-3a) | -8 | -8 | |
(3a-3) | -157 | -157 | |
(3-4) | |||
(4-1) | 125 | 125 | |
cycle | 40 | -40 |
Ceci permet notamment de calculer le coefficient de performance du cycle (COP), défini comme le rapport de l'effet utile (la chaleur extraite à l'évaporateur) à l'énergie payante (ici le travail du compresseur). Il vaut 3,14.
Prise en compte des écarts par rapport aux évolutions de référence
Ce cycle s'écarte de celui d'une machine réelle sur plusieurs points :
la compression réelle n'est pas parfaite, de telle sorte que le travail de compression est plus élevé que celui auquel conduirait l'adiabatique réversible ;
pour éviter d'aspirer du liquide dans le compresseur, ce qui risquerait de le détériorer car le liquide est incompressible, le gaz est surchauffé de quelques degrés (typiquement 5 °C) au-dessus de la température de saturation avant d'entrer dans le compresseur ;
avant d'entrer dans le détendeur, le liquide est sous-refroidi de quelques degrés (typiquement 5 °C) ; cela permet d'une part de s'assurer que cet organe n'est pas alimenté avec de la vapeur, et d'autre part d'augmenter les performances du réfrigérateur.
Comme nous l'avons expliqué, la compression réelle est caractérisée par un rendement isentropique, défini comme le rapport du travail de la compression réversible au travail réel.
Pour trouver le point 2' réel, on détermine donc la valeur du travail
 s mis en œuvre dans le compresseur parfait et on la divise par
s mis en œuvre dans le compresseur parfait et on la divise par
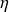 , ce qui donne la valeur du travail réel
, ce qui donne la valeur du travail réel
 .
.
Comme
 = h2' – h1, l'enthalpie du point 2' est égale à celle du point 1 plus
= h2' – h1, l'enthalpie du point 2' est égale à celle du point 1 plus
 .
.
Dans le cas présent, en prenant
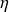 = 0,75, on a :
= 0,75, on a :
 s = h2 – h1 = 40 kJ/kg
s = h2 – h1 = 40 kJ/kg
 =
=
 s/
s/
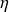 = 40/0,75 = 53
= 40/0,75 = 53
h2' = 391 + 53 = 444 kJ/kg
Le cycle modifié pour tenir compte de la surchauffe, du sous-refroidissement et des irréversibilités du compresseur est représenté figure ci-dessous (le cycle précédent est représenté en tiretés).

Le COP de la machine est bien entendu modifié : il baisse à 2,57 du fait des irréversibilités dans le compresseur.
L'intérêt du sous-refroidissement peut très facilement être montré dans le diagramme (h, ln(P)), car, pour un même travail de compression, l'effet utile augmente d'autant plus que le sous-refroidissement est important, ce qui a pour effet d'augmenter le COP. Il est toutefois limité par la nécessité de disposer d'un fluide de refroidissement.