Bilans enthalpiques
ÉTABLISSEMENT DES BILANS ENTHALPIQUES
Nous avons vu que, dans les processus industriels, les opérations se déroulent généralement en continu, c'est-à-dire en système ouvert[1][1]. Ce sont donc les expressions enthalpiques du premier principe qui s'appliquent le plus souvent.
Bien que celui-ci soit connu de tous ou presque, l'expérience prouve que sa mise en application peut poser quelques difficultés. Il ne s'agit pourtant que d'être capable d'appliquer la loi de conservation des grandeurs énergétiques extensives[2] (travail utile[3], chaleur échangée avec l'extérieur Q, débit d'enthalpie du ou des fluides mis en jeu) à un volume de contrôle bien choisi, qui le plus souvent n'est autre que le système délimité par les frontières du composant étudié. Compte tenu du premier principe, l'enthalpie est une grandeur conservative, et le premier principe se simplifie, les termes de génération et de consommation disparaissant, pour devenir :
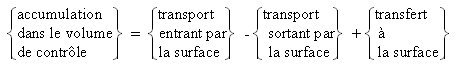
Si l'on fait l'hypothèse que le régime est permanent, ce qui est le plus souvent le cas, il n'y a pas d'accumulation nette dans le volume de contrôle, et cette équation se résume à :

Dans la plupart des cas, établir le bilan enthalpique demande ainsi seulement de comptabiliser les flux aux frontières de chaleur, de travail utile[3] et d'enthalpie.
Examinons à titre d'exemple le cas d'un turbocompresseur adiabatique de turbine à gaz, aspirant de l'air dans l'atmosphère au repos, et débitant dans la chambre de combustion de la machine.
Le volume de contrôle correspond dans ce cas à la géométrie du compresseur, délimité en amont et en aval par ses brides de raccordement.
Le bilan massique est très simple à établir, car, en notant d'un indice 1 l'entrée dans le compresseur, et 2 la sortie :
m1 = m2 en régime permanent
La machine étant adiabatique, il n'y a pas d'échange de chaleur avec l'extérieur, et donc Q = 0. A l'aspiration comme au refoulement, la vitesse de l'air est faible, et son énergie cinétique négligeable. Le bilan enthalpique de cette machine est particulièrement simple : Δh =
 . L'enthalpie communiquée au fluide est égale au travail reçu sur l'arbre.
. L'enthalpie communiquée au fluide est égale au travail reçu sur l'arbre.
Si le compresseur est refroidi, le bilan se complique un peu. Si la chaleur échangée avec l'extérieur est Q < 0, on a : Δh =
 + Q. L'enthalpie communiquée au fluide est égale (en valeur absolue) à la différence entre le travail reçu sur l'arbre et la chaleur extraite.
+ Q. L'enthalpie communiquée au fluide est égale (en valeur absolue) à la différence entre le travail reçu sur l'arbre et la chaleur extraite.
Considérons maintenant un exemple un peu plus complexe, relatif aux systèmes fermés. Il s'agit de la combustion dans un moteur diesel, modélisée comme étant la succession de deux combustions élémentaires (cycle dit mixte) : en premier lieu à volume constant, ensuite à pression constante.
Le bilan massique est cette fois un peu plus compliqué, mc étant la masse de combustible injecté pendant chaque phase de la combustion : m2 = m1 + mc
Le volume de contrôle est dans ce cas l'ensemble cylindre, culasse et piston. Le moteur étant refroidi par de l'eau, les combustions ne sont pas adiabatiques.
La première phase de combustion ayant lieu à volume constant, elle ne met en jeu aucun travail (W = 0), et le bilan énergétique devrait ici s'écrire
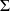 ΔUi = Q, la sommation étant effectuée sur toutes les espèces présentes, supposées être des gaz idéaux. Une première difficulté existe ici, car cette équation suppose que le calcul de l'énergie interne des gaz présents dans la chambre soit fait en tenant compte de l'avancement de la réaction de combustion, c'est-à-dire en considérant l'évolution des variables chimiques.
ΔUi = Q, la sommation étant effectuée sur toutes les espèces présentes, supposées être des gaz idéaux. Une première difficulté existe ici, car cette équation suppose que le calcul de l'énergie interne des gaz présents dans la chambre soit fait en tenant compte de l'avancement de la réaction de combustion, c'est-à-dire en considérant l'évolution des variables chimiques.
Cependant il est très rare dans la pratique industrielle que l'on opère ainsi : l'énergie interne (ou l'enthalpie) d'un gaz idéal est généralement définie par rapport à la référence standard de 1 bar et 298 K, pour une composition donnée.
Pour tourner cette difficulté, on a coutume, bien que cela soit formellement en contradiction avec le premier principe, de réintroduire un peu artificiellement dans les équations de bilan un terme de génération d'énergie dans le volume, qui correspond à la chaleur Qr (> 0) libérée par la réaction de combustion. Cette manière de faire permet de ne pas tenir compte des variables chimiques, et donc de sensiblement simplifier le formalisme.
Pour la phase de combustion à pression constante, le piston est en mouvement et produit un certain travail utile W qu'il faut aussi introduire dans le bilan.
APPLICATION AUX PROCESSUS INDUSTRIELS
C étant la vitesse du fluide, le premier principe appliqué à un composant traversé par un débit unitaire de fluide s'exprime, en unités massiques, sous la forme :
Nous avons déjà indiqué que, pour la plupart des machines thermiques, le terme gΔz (travail des forces de pesanteur) est négligeable. Dans de nombreux cas, la variation d'énergie cinétique ΔK reste faible vis à vis des autres variations (sauf bien entendu dans des cas spéciaux tels que les réacteurs d'avion, certains aubages de turbomachines ou organes de détente).
Dans ces conditions, la somme du travail reçu ou fourni et de la chaleur échangée avec l'extérieur par le composant est égale à la variation d’enthalpie du fluide qui le traverse.
Cette relation fondamentale explique pourquoi, dans les appareils industriels, il est pratiquement impossible de mettre en œuvre à la fois une forte puissance mécanique et un flux calorifique important.
les composants appelés à transférer de la chaleur d'un fluide à un autre (échangeurs de chaleur) nécessitent de grandes surfaces d'échange, les flux thermiques leur étant proportionnels. Des considérations techniques et économiques amènent à adopter des dispositifs purement statiques. Par exemple, de grands faisceaux de tubes en parallèle, parcourus intérieurement par un fluide pendant que l'autre circule à l'extérieur.
 est alors nul en raison de l'absence de parois mobiles.
est alors nul en raison de l'absence de parois mobiles.les machines réalisant la compression ou la détente d'un fluide ont une conception très compacte pour des raisons de poids, d'encombrement et de coût. Pour les mêmes raisons, elles tournent très vite (plusieurs milliers de tours par minute). Chaque parcelle de fluide y séjourne très peu de temps. Par ailleurs les coefficients d’échange thermique des gaz ont des valeurs faibles. Les courts temps de séjour, les petites surfaces de contact fluide-paroi, et les faibles coefficients d’échange font que l'échange de chaleur est minime et que le fonctionnement de ces machines est pratiquement adiabatique.
il existe une classe d'appareils où
 et Q sont nuls tous les deux : ce sont les détendeurs statiques tels que vannes, filtres... La transformation correspondante s’appelle un "laminage" isenthalpique ou encore une détente flash.
et Q sont nuls tous les deux : ce sont les détendeurs statiques tels que vannes, filtres... La transformation correspondante s’appelle un "laminage" isenthalpique ou encore une détente flash.
En résumé, l'application de cette équation conduit aux conclusions suivantes :
dans un échangeur de chaleur, la chaleur Q cédée ou fournie par un fluide à l'autre est égale à sa variation d'enthalpie Δh ;
dans une machine adiabatique, le travail utile
 est égal à la variation d'enthalpie du fluide Δh ;
est égal à la variation d'enthalpie du fluide Δh ;un laminage conserve l'enthalpie (Δh = 0).
Pour le calcul des transformations, ces conclusions sont très importantes en pratique puisqu'elles indiquent que dans la plupart des composants des machines industrielles, les échanges thermiques et mécaniques sont découplés. Elles expliquent aussi pourquoi l'enthalpie est une fonction d'état[4] très utilisée dans les transformations en système ouvert[1] : la variation d'enthalpie du fluide correspond selon les cas à l'énergie mécanique ou thermique mise en jeu.
