Fil d'Ariane sur les compresseurs volumétriques
Présentation
Dans ce fil d'Ariane pédagogique sur les compresseurs volumétriques, après avoir succinctement rappelé ce que sont de tels composants et donné quelques éléments de théorie sur la manière dont ils peuvent être calculés, nous détaillons le calcul et le dimensionnement d'un compresseur à piston servant à alimenter un réservoir de stockage d'air comprimé.
Il s'agit d'un exemple destiné à bien faire comprendre quels sont les problèmes posés et comment ils peuvent être résolus, sans que le système d'ensemble soit trop compliqué. Pour des spécialistes, il paraîtra sans doute un peu simpliste, mais pour des débutants, il se révèle déjà relativement difficile à traiter complètement.
Il fait appel à la version 2.7 de Thermoptim actuellement en cours de développement.
La carte ci-dessous résume l'essentiel des notions qui seront abordées ici.
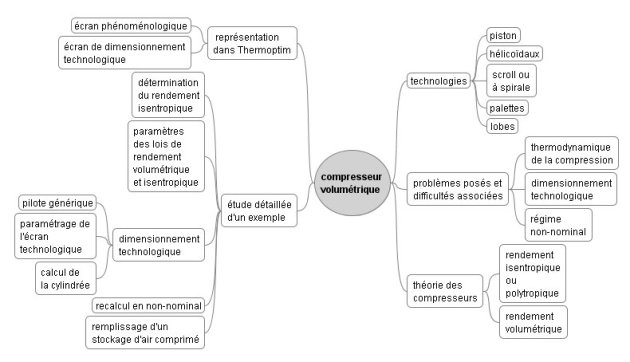
Qu'est-ce qu'un compresseur ?
Sur le plan fonctionnel, les compresseurs sont des appareils qui servent à augmenter la pression des fluides qui les traversent.
Les compresseurs sont utilisés pour de nombreuses applications industrielles, pour la réfrigération, le conditionnement d'air, le transport du gaz naturel...
Une mention particulière doit être faite des compresseurs à air, utilisés comme source de puissance dans les chantiers de travaux publics et du bâtiment ainsi que dans les usines, les outils pneumatiques présentant de nombreux avantages. L'exemple que nous présentons ici porte sur un tel type d'appareil.
Sur le plan technologique, les compresseurs peuvent être regroupés en deux grandes classes :
les compresseurs volumétriques, dans lesquels le fluide est emprisonné dans un volume fermé que l'on réduit progressivement pour réaliser la compression ;
et les turbocompresseurs, qui utilisent un principe différent : la compression y est obtenue en convertissant en pression l'énergie cinétique communiquée au fluide par des aubages mobiles.
Nous nous limiterons dans ce qui suit à l'étude des compresseurs volumétriques, parmi lesquels on distingue généralement :
les compresseurs à piston
les compresseurs hélicoïdaux
les compresseurs scroll ou à spirale
les compresseurs à palettes
les compresseurs à lobes
Un compresseur volumétrique se caractérise par l'encapsulation, ou emprisonnement, du fluide qui le traverse dans un volume fermé que l'on réduit progressivement. Un retour de ce fluide dans le sens des pressions décroissantes y est empêché par la présence d'une ou plusieurs parois mobiles. Dans ce type de machine, l'énergie cinétique communiquée au fluide ne joue généralement aucun rôle utile, contrairement à ce qui se passe dans les turbomachines.
De par leur conception, les compresseurs volumétriques conviennent particulièrement bien pour traiter les débits de fluide relativement faibles, éventuellement très variables, et sous des rapports de pression relativement importants.
Leur principe de fonctionnement est le suivant : une masse fixe de gaz à la pression d'aspiration P1 est emprisonnée dans une enceinte de volume variable. Pour augmenter la pression, ce volume est progressivement réduit, d'une manière qui diffère selon la technique utilisée.
Dans un compresseur à piston, l'enceinte est le volume délimité par un cylindre, l'une de ses bases qui est fixe, et l'autre qui est un piston mobile dans l'alésage du cylindre, entraîné par un système bielle-manivelle.

En fin de compression, l'enceinte est mise en communication avec le circuit de refoulement, pour que le gaz comprimé à la pression P2 puisse sortir. Une nouvelle masse de gaz à la pression P1 est alors aspirée dans les canalisations amont, et ainsi de suite, le fonctionnement de la machine étant cyclique.
Les organes qui commandent le refoulement ou l'admission sont, dans les compresseurs à piston, des clapets automatiquement actionnés par les différences de pression entre l'enceinte et les tubulures de refoulement ou d'admission.
On désigne par cylindrée le volume Vs balayé par le piston entre ses deux positions extrêmes, et par espace mort e Vs le volume minimal de l'enceinte de compression. Dans les réalisations courantes, e est de l'ordre de 3 à 5 %.
Du fait de l'existence de l'espace mort, les compresseurs volumétriques présentent une caractéristique particulière : leur cylindrée apparente est inférieure à leur cylindrée géométrique. Une certaine masse de fluide reste enfermée dans le compresseur en fin de refoulement, venant ainsi réduire le volume utile de la machine. On caractérise cette réduction de cylindrée par une grandeur lambda appelée rendement volumétrique.
Un faible rendement volumétrique n'est pas en soi pénalisant sur le plan énergétique : il signifie simplement que le débit-masse qui traverse le compresseur est plus faible que celui qui correspondrait théoriquement à la cylindrée. Il est en revanche pénalisant sur le plan économique, puisque, pour un cahier des charges donné, il conduit à surdimensionner la cylindrée, et donc à un investissement plus élevé.
Typologie des problèmes posés et difficultés associées
L'étude des compresseurs dans un système énergétique présente des niveaux de difficulté très différents selon les objectifs que l'on poursuit.
L'approche la plus élémentaire consiste à calculer la température de sortie lorsque le rapport de compression et le rendement isentropique sont connus. Si le débit mis en jeu est lui aussi connu, le travail de compression s'en déduit directement.
Le problème inverse se résout lui aussi simplement : connaissant les états d'entrée et de sortie du compresseur, il s'agit de déterminer le rendement isentropique de l'appareil.
Pour aller plus loin et déterminer le rendement isentropique et le débit qui traverse une machine de cylindrée donnée, il faut effectuer des calculs plus compliqués, qui requièrent une connaissance approfondie du fonctionnement des compresseurs.
Nous appellerons dimensionnement technologique les calculs qui permettent de déterminer la cylindrée d'un compresseur connaissant les lois donnant ses rendements volumétrique et isentropique.
Il s'agit d'un problème général dans les études de systèmes énergétiques : tant que l'on se contente d'effectuer des études de cycles sans chercher à dimensionner les composants sur le plan géométrique, les calculs restent beaucoup plus simples que lorsque l'on désire analyser finement leur comportement interne.
Une fois la cylindrée déterminée, ce qui permet de caractériser le compresseur de manière détaillée sur le plan géométrique, un autre problème reste à traiter : celui de son comportement lorsque ses conditions de fonctionnement diffèrent de celles qui ont servi à le dimensionner.
Nous qualifions cette problématique d'étude de son comportement en régime non-nominal.
Elle peut être d'un niveau de complexité supérieur à celle du dimensionnement technologique, du fait qu'elle peut demander la résolution de systèmes d'équations non linéaires de rang élevé lorsque plusieurs composants sont couplés entre eux.
Eléments de théorie de la compression
Les machines réalisant la compression ou la détente d'un fluide ont une conception très compacte pour des raisons de poids, d'encombrement et de coût. Pour les mêmes raisons, elles tournent très vite (plusieurs milliers de tours par minute). Chaque parcelle de fluide y séjourne très peu de temps.
Par ailleurs les coefficients d’échange thermique des gaz ont des valeurs faibles. Les courts temps de séjour, les petites surfaces de contact fluide-paroi, et les faibles coefficients d’échange font que l'échange de chaleur est minime et que le fonctionnement de ces machines est pratiquement adiabatique.
Dans ces conditions, la transformation idéale de référence est l'adiabatique réversible, c'est à dire la transformation isentropique.
Toutefois, dans une machine réelle, des irréversibilités prennent place, essentiellement dues aux frottements visqueux et aux chocs. Elles ont pour conséquence d'augmenter la température du fluide et son entropie. Dans un diagramme entropique, l'allure de l'évolution s'écarte ainsi de l'isentropique théorique (cf. figure ci-dessous).
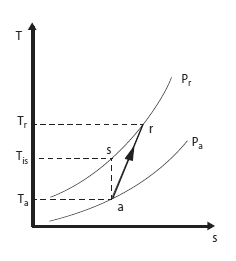
Compression adiabatique réelle
Pour calculer le travail mis en jeu dans une compression adiabatique réelle, il y a deux manières d'opérer :
la première consiste à introduire un rendement appelé rendement isentropique (ou adiabatique), déterminé expérimentalement, qui est défini comme comme le rapport entre le travail de compression isentropique et le travail de compression réel ;
la deuxième manière consiste à introduire la notion de polytropique. Nous renvoyons le lecteur intéressé à la fiche thématique sur les compresseurs.
Pertes dans les compresseurs volumétriques
Dans un compresseur volumétrique, deux types de pertes sont généralement considérées :
celles qui viennent réduire la capacité du compresseur, qui sont représentées comme nous l'avons dit par son rendement volumétrique ;
celles qui proviennent des irréversibilités thermodynamiques et mécaniques qui prennent place en son sein, qui sont le plus souvent caractérisées par son rendement isentropique.
En l'état actuel de nos connaissances, la détermination de ces deux types de pertes ne peut être effectuée que de manière globale et expérimentale.
Rendement volumétrique lambda
L'analyse et l'expérimentation ont montré que lambda peut s'écrire sous la forme suivante, les deux pertes les plus importantes étant en premier lieu beta3, puis beta1 :
beta1 est la perte due à l'espace mort ;
beta2 est la perte due aux pertes de charge dans les collecteurs d'admission et de refoulement ;
beta3 est la perte due aux effets de paroi (shunt thermique) ;
beta4 est la perte due aux défauts d'étanchéité (au niveau des segments des pistons et des clapets) ;
beta5 est la perte due aux pertes de charge dans les clapets d'admission et de refoulement.
Il existe en particulier un taux de compression limite au delà duquel le compresseur ne fournit plus aucun débit de fluide. Physiquement, cela signifie qu'en fin de détente, la masse contenue dans l'espace mort occupe à la pression Pasp l'ensemble du volume du cylindre, de telle sorte que le compresseur ne peut plus rien aspirer.
L'ensemble de toutes les pertes se conjugue pour donner au rendement volumétrique des lois de variation par rapport au taux de compression et par rapport à la vitesse de rotation qui ont les allures données dans les figures ci-dessous.
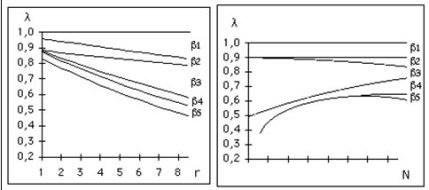
A taux de compression constant, elles font apparaître un optimum à vitesse assez élevée. En effet, à faible vitesse, les effets de paroi (beta3) et fuites (beta4) sont relativement importants, et faiblissent quand la vitesse augmente. En revanche, à vitesse élevée, les pertes de charge dans les collecteurs (beta2) et surtout les clapets beta5) jouent un rôle croissant.
Rendement isentropique eta
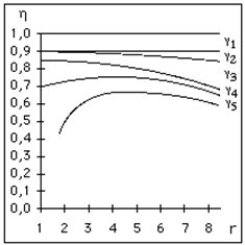
Trois sources de pertes liées aux précédentes influent principalement sur le rendement isentropique, qui peut s'écrire, les termes gamma1 à 5 correspondant aux mêmes phénomènes que précédemment :
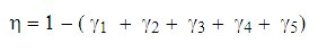
les effets de paroi (gamma3) sont très pénalisants, car ils augmentent fortement le travail de compression en déformant l'isentropique ;
les pertes dues aux clapets (gamma5) viennent ensuite, suivies des pertes par défaut d'étanchéité (gamma4).
A vitesse donnée, l'allure de la variation du rendement de compression en fonction du rapport isentropique est donnée figure ci-dessous. Elle montre l'existence d'un maximum vers des taux de compression plutôt faibles (3 à 5).
A taux de compression donné, le rendement isentropique passe, lorsque la vitesse varie, par un maximum voisin de celui du rendement volumétrique.
L'ensemble de ces phénomènes est extrêmement complexe à modéliser, de telle sorte qu'on se contente généralement d'ajuster des modèles numériques pour représenter le comportement des compresseurs volumétriques, comme nous le verrons plus loin.
Généralement, le rendement volumétrique présente une décroissance sensiblement linéaire en fonction du taux de compression.
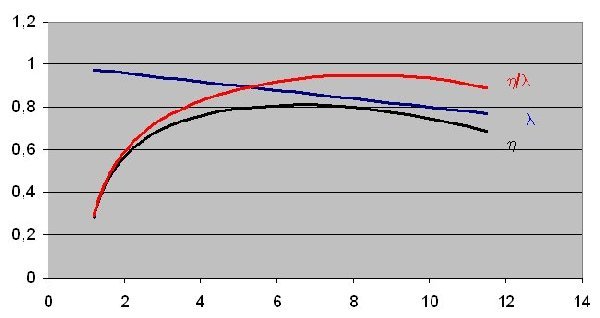
La figure ci-dessous montre l'allure du rendement isentropique et du rendement volumétrique pour un compresseur à piston.
Méthode de calcul pratique et représentation dans Thermoptim
Détermination de l'état de sortie du compresseur
Si l'on retient l'approche par rendement isentropique, bien adaptée pour un compresseur volumétrique, la séquence de règles de calcul d'une compression peut s'énoncer de la manière suivante :
1) on commence par calculer l'entropie à l'aspiration s(Pa, Ta) ;
2) il faut ensuite inverser en Ts l'équation s(Pr, Ts) = s(Pa, Ta) ;
3) on peut alors déterminer le travail correspondant à l'évolution isentropique Dhs = h(Pr, Ts) - h(Pa, Ta) ;
4) on en déduit l'enthalpie de sortie hr = h(Pa, Ta) + Dhs/h , eta étant le rendement isentropique ;
5) enfin, on obtient la température de refoulement en inversant en Tr l'équation h(Pr, Tr) = hr.
Représentation dans Thermoptim
L'icône d'un compresseur dans Thermoptim est :
L'écran (phénoménologique) d'un compresseur propose plusieurs paramétrages thermodynamiques possibles :
si la compression est adiabatique, on peut choisir une approche isentropique ou polytropique. Il faut alors entrer la valeur du rendement isentropique ou polytropique ;
si la compression n'est pas adiabatique, le mode de calcul est alors impérativement polytropique. Il faut entrer les valeurs du rendement et de l'exposant polytropiques.
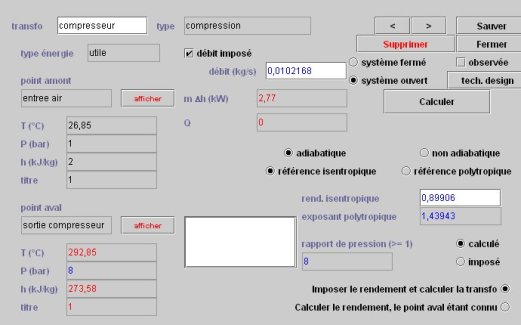
Ecran d'un compresseur dans Thermoptim
Comme nous l'avons indiqué plus haut, on peut généralement faire l'hypothèse que la compression est adiabatique.
L'utilisation de cet écran suppose que l'on fournisse d'une part la valeur du rendement isentropique (dans notre cas) ou polytropique, et d'autre part celle du débit, soit directement, soit par le biais du composant situé en amont s'il en existe un.
Lorsqu'on cherche à représenter avec précision le comportement d'un compresseur donné, il est nécessaire de le caractériser par :
sa cylindrée ;
sa loi de rendement volumétrique ;
sa loi de rendement isentropique.
Loi de rendement volumétrique
Compte tenu de l'allure des pertes présentée précédemment, une loi affine suffit pour représenter l'évolution du rendement volumétrique en fonction du rapport de compression :
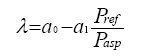
Loi de rendement isentropique
Pour représenter correctement le rendement isentropique, il faut plus de paramètres. La loi que nous retiendrons fait appel à 5 :
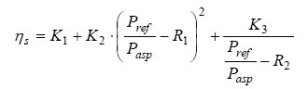
Pour pouvoir dimensionner un compresseur, il est nécessaire de connaître ces lois. Une identification de leurs paramètres peut généralement être faite sur la base des données fournies par le constructeur.
Etude progressive et détaillée d'un exemple de compresseur volumétrique
Pour illustrer ce qui vient d'être présenté, nous allons étudier le comportement d'un compresseur volumétrique à air qui remplit un stockage d'air comprimé de volume donné à pression variable. L'air comprimé est refroidi avant stockage grâce à un échangeur à eau du type de celui qui est présenté dans le fil d'Ariane sur les échangeurs , auquel nous vous renvoyons pour plus de détails.
Ce compresseur aspire un débit d'air de 0,66 kg/mn (11,738 g/s) à 1 bar et 26,85 °C, et le comprime à 5 bars.
Détermination du rendement isentropique connaissant l'état de sortie
On souhaiterait connaître la valeur du rendement isentropique conduisant à une température de sortie égale à 275 °C.
Le système peut être facilement modélisé dans Thermoptim et conduit à un schéma du type de la figure ci-dessous, qui ne se distingue de celui étudié lors dans le fil d'Ariane sur les échangeurs que par l'ajout du compresseur.
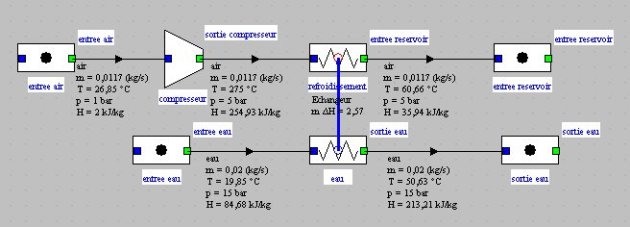
Pour déterminer le rendement isentropique conduisant à la température de sortie choisie, il faut sélectionner l'option "Calculer le rendement, le point aval étant connu", après avoir paramétré en conséquence le point "sortie compresseur", comme le montre la figure ci-dessous.
La valeur obtenue est eta = 0,69531.
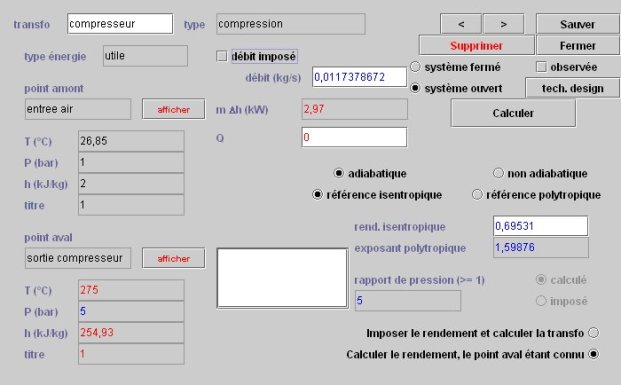
Dimensionnement du compresseur
Pour pouvoir dimensionner le compresseur, il faut comme nous l'avons vu disposer des paramètres des équations donnant les rendements volumétrique et isentropique.
Nous supposerons ici qu'ils ont pu être déterminés à partir de données fournies par le constructeur.
Le calcul d'un compresseur correspond aux étapes ci-dessous :
les rendements volumétrique et isentropique lambda et eta sont calculés à partir de leurs équations
si l'on connaît la vitesse de rotation, la cylindrée et le rendement volumétrique, le débit volumique peut être calculé : Vvol = lambda N Vs / 60
connaissant la masse volumique à l'aspiration v, on en déduit le débit massique : m = Vvol / v = lambda N Vs / 60 /v
En mode dimensionnement, on détermine la vitesse de rotation permettant de fournir le débit souhaité ou la cylindrée correspondant à une vitesse de rotation donnée. Le calcul est effectué en prenant en compte les pressions d'entrée et de sortie et la valeur du débit saisi dans le champ du débit du compresseur.
En régime non-nominal, le rapport de compression détermine lambda et eta, ce qui fixe le débit et la température de sortie compresseur.
Utilisation du pilote générique
Lorsque l'on se contente de vouloir effectuer le dimensionnement technologique d'un projet qui ne met en oeuvre que des composants du noyau de Thermoptim, leurs écrans technologiques peuvent être créés automatiquement en utilisant le pilote générique, sans avoir besoin d'en programmer un particulier.
Pour charger le pilote générique, ouvrez l'écran de pilotage à partir du menu Spécial du simulateur, et sélectionnez "generic techno design pilot ". Attention : le pilote générique demande que le schéma et le simulateur soient tous deux chargés dans Thermoptim.
Une fois l'écran du pilote générique ouvert, cliquez sur le bouton "Set the technological design screens".
Deux lignes apparaissent correspondant à l'échangeur et au compresseur, comme dans la figure ci-dessous. Sélectionnez-celle du compresseur.
Son type est par défaut Compression, et son TechnoDesign VolumCompr. Etant donné qu'il s'agit d'un compresseur volumétrique, ils conviennent parfaitement. Un double-clic sur cette ligne permettrait de changer le type de TechnoDesign, mais ce n'est pas ici nécessaire.
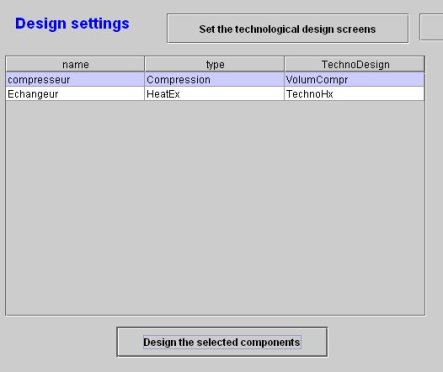
Vous pouvez accéder à l'écran de dimensionnement technologique du compresseur grâce au bouton "tech. design" situé au dessus du bouton "Calculer" de l'écran de la transfo compresseur.
Ecran de dimensionnement technologique
L'écran de dimensionnement technologique d'un compresseur volumétrique est donné figure ci-dessous.
Les champs bleus dans la partie gauche de l'écran technologique du compresseur permettent d'entrer les caractéristiques du compresseur :
deux paramètres pour la droite de rendement volumétrique a0 et alpha ;
cinq paramètres pour le rendement isentropique K1, K2, K3, R1 et R2 ;
la vitesse de rotation de référence (pour laquelle les cinq paramètres ont été déterminés) ;
ainsi que le volume balayé à pleine charge Vs (en m3).
Entrez dans ces champs les valeurs des caractéristiques, sélectionnez l'option "Calculate Vs", afin que Thermoptim sache que cette valeur doit être calculée, puis retournez dans l'écran du pilote générique, et cliquez sur "Design the selected components".
Les champs dans la partie droite de l'écran technologique affichent les valeurs calculées du rendement isentropique, du débit massique et du rendement volumétrique.
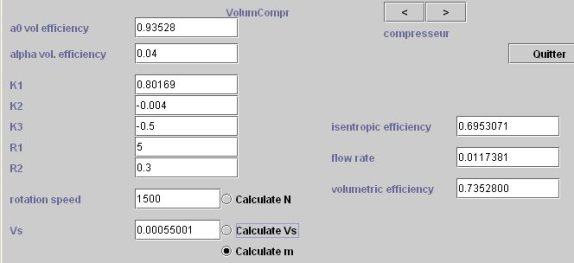
Ecran technologique du compresseur
La cylindrée (0,0055 m3) a été déterminée sur la base du débit entré dans la transfo du compresseur, et les autres valeurs à partir des caractéristiques saisies. Une fois la cylindrée recalculée, l'option "Calculate m" est sélectionnée, car cela correspond au mode de calcul normal de ce TechnoDesign.
Les fichiers correspondant à cet exemple sont disponibles pour téléchargement .
Nous n'avons pas parlé ici du dimensionnement de l'échangeur, qui est expliqué en détail dans la fiche d'Ariane sur les échangeurs.
Calculs en régime non-nominal
En régime non-nominal, on connaît ces caractéristiques, la vitesse de rotation et la cylindrée. Le rapport de compression et le volume massique à l'entrée permettent de calculer les nouvelles valeurs des rendements volumétrique et isentropique, et d'en déduire la température de sortie, le débit mis en jeu et le travail de compression correspondant.
Pour illustrer ce type de calculs, nous allons maintenant étudier le comportement du compresseur volumétrique à air que nous venons de présenter, lorsqu'on l'utilise pour remplir un stockage d'air comprimé de volume donné à pression variable.
Nous allons pour cela opérer en trois temps :
réaliser un pilote qui permettra d'automatiser le recalcul du compresseur muni de son échangeur de refroidissement, afin de simuler son comportement pour diverses valeurs de la pression de refoulement ;
identifier numériquement les paramètres de lois permettant d'exprimer les évolutions de la température de sortie compresseur,du débit mis en jeu et du travail de compression en fonction de la pression de refoulement
construire un tableur qui permettra d'étudier l'évolution de l'état du stockage d'air comprimé en fonction du temps
Rôle du pilote
Pour obtenir les résultats recherchés, il faut construire un pilote, dont l'écran peut avoir l'aspect ci-dessous. Il permet de faire varier le rapport de compression pour obtenir les évolutions des principales grandeurs lorsque la pression du réservoir varie, en opérant comme suit :
mise à jour de la pression de sortie du compresseur
calcul du rendement volumétrique du compresseur
calcul du rendement isentropique du compresseur
recalcul du compresseur et de la transfo aval
mise à jour des entrées et sorties de l'échangeur
détermination de U puis mise à jour de UA et recalcul de l'échangeur en mode non-nominal (en plusieurs itérations étant donné que U dépend des températures moyennes des fluides, et donc de celles de sortie)
mise à jour du simulateur et des affichages
Les résultats de la figure ci-dessous correspondent à un rapport de compression égal à 8. Le débit a un peu baissé, du fait de la loi de rendement volumétrique, et le rendement isentropique légèrement augmenté.
On notera que dans cet exemple le comportement du compresseur ne dépend pas, une fois le rapport de compression défini, de celui de l'échangeur situé en aval : il n'y a pas de couplage systémique, du moins pour un point de fonctionnement donné.
La conception du pilote en est facilitée : il n'y a pas à résoudre de système d'équations non linéaires de couplage.
Nous ne détaillerons pas ici la programmation du pilote, qui est expliquée dans le tome 4 du manuel de référence, auquel nous conseillons le lecteur intéressé de se reporter.
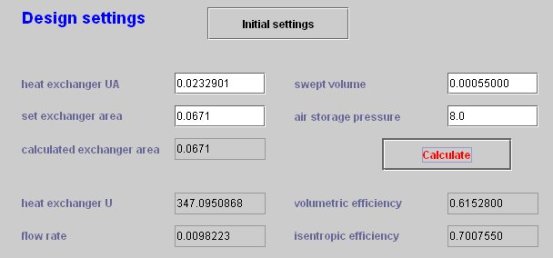
Exploitation des résultats de simulation
Une fois le pilote réalisé, il est très facile de faire varier le rapport de compression pour obtenir les évolutions des principales grandeurs lorsque la pression du réservoir varie.
Elles peuvent être exploitées avec la macro Excel de post-traitement des fichiers de simulation de Thermoptim présentée au tome 1 du manuel de référence. Il suffit pour cela de sauvegarder le fichier de projet sous un nom différent après chaque simulation, puis de charger ces fichiers dans la macro et d'en extraire les valeurs intéressantes.
La figure ci-dessous montre, en fonction de la pression du stockage, les évolutions du rendement isentropique du compresseur, du travail consommé, du débit d'air aspiré, de la température de l'air entrant dans le réservoir, de la charge de l'échangeur et de UA.
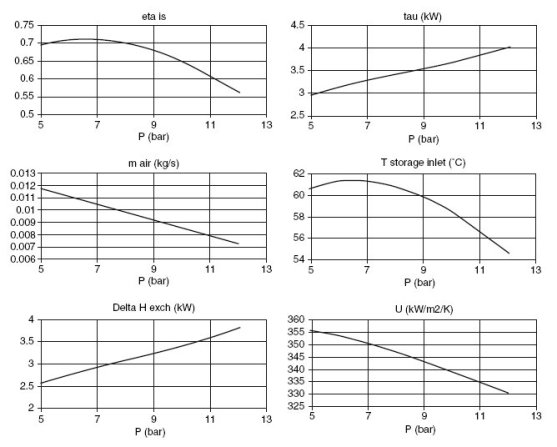
Influence de la pression de refoulement sur les performances du compresseur
Entre 5 et 12 bars,
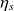 et U varient respectivement de 22 % de 7 %. Comme l'allure des courbes est dans certains cas loin d'être linéaire, des approches trop simplistes ne suffisent pas, ce qui démontre bien l'intérêt de notre démarche.
et U varient respectivement de 22 % de 7 %. Comme l'allure des courbes est dans certains cas loin d'être linéaire, des approches trop simplistes ne suffisent pas, ce qui démontre bien l'intérêt de notre démarche.
Utilisation du modèle pour simuler le remplissage d'un stockage d'air comprimé
Les résultats de la figure ci-dessus peuvent être utilisés pour simuler le remplissage d'un stockage d'air comprimé. Thermoptim ne fournissant de résultats que pour un régime stabilisé, le plus simple est de développer un second modèle, résolu sous Excel.
Ses équations sont les suivantes :
la masse M d'air contenue dans le stockage est égale à la masse initiale plus l'intégrale du débit ;
l'énergie interne U est égale à l'énergie interne initiale plus l'intégrale du produit du débit par l'enthalpie de l'air sortant du refroidisseur, moins l'intégrale des pertes par convection avec l'air ambiant ;
la température du stockage est déduite de son énergie interne ;
la pression est déterminée par la loi des gaz idéaux.
Pour connaître le débit, le travail de compression et la température de l'air en entrée de stockage, il suffit de faire des régressions polynomiales à partir des simulations effectuées précédemment avec Thermoptim. Les équations obtenues sont, en fonction du rapport de compression r :

L'allure des résultats est donnée figure ci-dessous, pour un stockage d'un demi m3 (diamètre 80 cm, longueur 1 m), alimenté par un compresseur de cylindrée Vs = 0,55 l. La pression et la température dans le stockage, sa masse et le travail à fournir au compresseur sont affichés en fonction du temps exprimé en secondes.
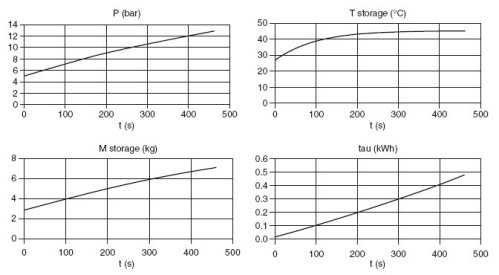
Charge du stockage d'air comprimé
Les fichiers correspondant à cet exemple sont disponibles pour téléchargement .
