Gaz parfaits et idéaux
Gaz parfaits et idéaux
Beaucoup de fluides thermodynamiques en phase vapeur peuvent être assimilés à des gaz idéaux, dans un large domaine de températures et de pressions. Il faut notamment que la combinaison température-pression s'écarte suffisamment de la zone de condensation possible (c'est-à-dire que la pression ne soit pas "trop" élevée, ni la température "trop" basse). De telles conditions sont couramment réalisées pour des gaz dits "permanents" tels que, à pression et température ambiantes, l'hydrogène, l'oxygène, l'azote, le mélange oxygène-azote qui constitue l'air sec... Même la vapeur d'eau dans l'atmosphère se comporte pratiquement comme un gaz idéal tant que sa pression partielle reste modérée.
Le modèle de gaz idéal est basé sur l'hypothèse que les interactions moléculaires du gaz peuvent être négligées, à l'exception des collisions entre elles. La théorie cinétique des gaz permet alors d'expliquer le comportement macroscopique du gaz à partir de considérations mécaniques et statistiques sur les mouvements de ses molécules.
L'hypothèse fondamentale des gaz idéaux est que leur énergie interne (ainsi que leur enthalpie) est indépendante de la pression. Étant donné que tous les gaz réels sont liquéfiables, il n'existe pas de gaz rigoureusement idéal ou parfait. Ces notions sont cependant fondamentales, car la détermination pratique de l'état d'un fluide réel se fait toujours par référence au gaz idéal ou parfait correspondant, dont son comportement se rapproche à très basse pression et /ou très haute température.
Plus précisément, pour représenter l'état d'un fluide, on utilise en fonction de la précision désirée, une cascade de modèles de complexité croissante, le plus simple étant celui du gaz parfait, les plus élaborés correspondant aux modèles de fluides réels.
Rappelons qu'une séance Diapason est consacrée à la présentation des propriétés des gaz idéaux . Elle constitue un résumé de cette partie.
Équation d'état des gaz idéaux
Les équations des gaz parfaits et des gaz idéaux sont très proches, les premiers n'étant en fait qu'un cas particulier des seconds. L'équation d'état d'un gaz idéal peut s'écrire :
Pv = rT (1)
avec r = R/M (kJ/kg/K)
R est la constante universelle = 8,314 (kJ/kmol/K)
M est la masse molaire du gaz (kg/kmol)
Selon les unités employées, l'équation (1) prend différentes formes :
en unités massiques : P v = r T
en unités molaires : P vm = R T
Rapportée au volume total V occupé par le fluide, n étant le nombre de kilomoles :
en unités massiques : P V = m r T
en unités molaires : P V = n R T
On démontre que l'équation (1) a notamment pour conséquence que l'énergie interne et l'enthalpie d'un gaz idéal ne dépendent que de sa température, et que
r = cp - cv
On a donc :
cv = du/dT (J/kg/K)
cp = dh/dT (J/kg/K)
On appelle gaz parfait un gaz idéal dont les capacités thermiques massiques cp et cv sont constantes.
Pour un tel gaz, l'énergie interne et l'enthalpie sont des fonctions affines de la température. On notera que d'autres auteurs appellent gaz parfait ce que nous appelons gaz idéal. Dans ce cas, ils doivent à chaque fois préciser si la capacité thermique du gaz dépend ou non de la température.
L'hypothèse des gaz parfaits (cp et cv constants) n'est en toute rigueur vérifiée que pour les gaz monoatomiques (qui ne comportent aucun mode de rotation ni de vibration moléculaire). Elle est d'autant moins satisfaisante que la molécule de gaz comporte davantage d'atomes (et donc de modes vibratoires possibles).
La thermodynamique statistique permet de déterminer les valeurs des capacités thermiques molaires des gaz monoatomiques et diatomiques.
Pour les premiers, on obtient :
Cp = 5/2 R = 20, 785 kJ/kmol Cv = 3/2 R = 12,471 kJ/kmol
Pour les gaz diatomiques usuels, à la température ambiante, on obtient :
Cp = 7/2 R = 29,1 kJ/kmol Cv = 5/2 R = 20, 785 kJ/kmol
La figure ci-dessous donne les évolutions de Cp pour quelques gaz typiques mono-, bi- et tri-atomiques.
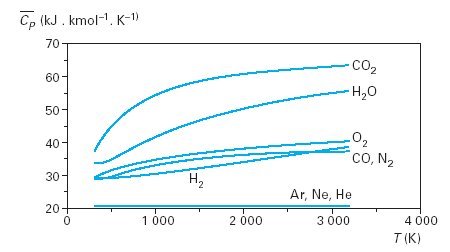
Détermination pratique de l'état d'un gaz parfait
Deux paramètres seulement suffisent pour définir un gaz parfait : soit ses capacités thermiques massiques à pression et volume constants, soit l'une d'entre elles et la valeur de sa masse molaire M, soit encore les valeurs de M et de g, rapport de cp à cv.
En vertu des hypothèses, Pv = rT, cp - cv = r, et cp et cv constantes, on peut très simplement calculer l'énergie interne u et l'enthalpie h du gaz à partir d'un état de référence quelconque T0.
u = u0 + cv (T - T0) et h = h0 + cp (T - T0) (2)
Tds = du + Pdv
ds = 1/T du + p/T dv
qui permet de calculer aisément l'entropie du fluide : ds = cp/T dT + r/v dv
s = s0 + cp ln(P/P0) + cv ln(v/v0)
s = s0 + cv ln(T/T0) + r ln(v/v0) (3)
s = s0 + cp ln(T/T0) - r ln(P/P0)
Le choix du point de référence est arbitraire et dépend des conventions.
Les caractéristiques (M, cp, cv, r, g) de quelques corps sont indiquées dans le tableau ci-dessous.
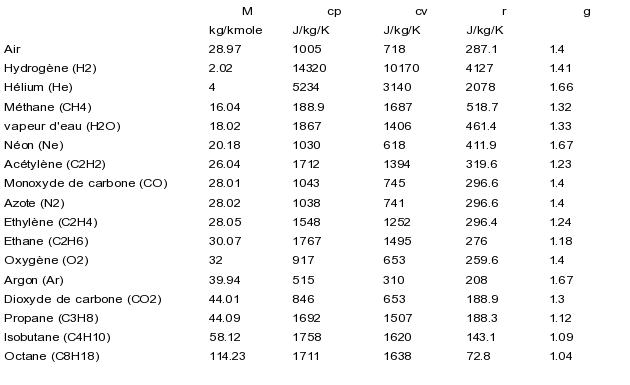
Détermination pratique de l'état d'un gaz idéal
Un gaz idéal diffère d'un gaz parfait en ce que ses capacités thermiques ne sont pas constantes, mais dépendent uniquement de la température.
Le plus souvent, on représente Cp par un ajustement polynomial d'ordre n en T, sous la forme (soit en unités molaires, comme ci-dessous, soit en unités massiques) :
Cp =
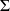 Cpi Ti (4)
Cpi Ti (4)
C’est cette solution qui a été retenue dans Thermoptim, avec un développement à 7 termes du type suivant :
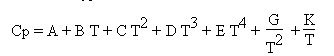
On en déduit Cv par Cv = Cp - R, et on passe aux variables massiques cp et cv en divisant ces valeurs par la masse molaire du corps.
En pratique, si l'on ne dispose pas d'un logiciel de calcul des propriétés des corps, et que l'on cherche à déterminer l'évolution d'un gaz idéal sur une plage restreinte de variation en température, il est possible de l'assimiler à un gaz parfait, ce qui permet d'utiliser l'ensemble des résultats établis pour ces derniers, à condition de calculer sa capacité thermique massique à la température moyenne de la transformation. Bien entendu, ceci n'est valable qu'en première approximation, mais la perte de précision est compensée par une grande simplification des calculs.
A partir d'une expression polynomiale cp ou cv = f(T), il est facile de calculer u, h ou s en intégrant leurs relations différentielles, ce qui conduit à :
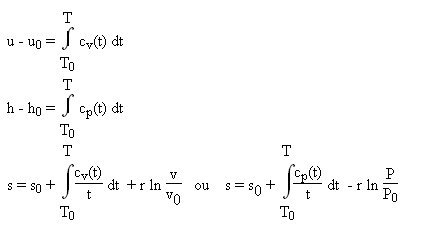
Équation des isentropiques
Dans de nombreux compresseurs ou turbines, le fluide subit une évolution proche de l'isentropique, qui constitue ainsi la référence par rapport à laquelle la transformation réelle est calculée. Les équations des isentropiques revêtent donc une importance particulière.
En posant s = s0 = Cste, on trouve, pour les gaz parfaits :
ou encore, sous forme différentielle :
dP/P +
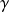 dv/v = 0 (9)
dv/v = 0 (9)
Pour un gaz idéal, l'équation des isentropiques ne prend pas une forme aussi simple que pour un gaz parfait. Le formalisme est plus complexe, mais il reste cependant tout à fait utilisable en pratique, les variables pression et température pouvant être séparées.
On obtient ici une généralisation de l'expression pour le gaz parfait :
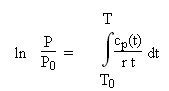
Mélanges de gaz idéaux
Dans de nombreuses applications pratiques, on a affaire non pas à des gaz purs, mais à des mélanges de gaz, dont la composition peut varier. C’est notamment le cas dans un cylindre de moteur à combustion interne : la composition des fumées évolue au fur et à mesure que se déroule la combustion.
La loi de Dalton énonce un résultat capital : un mélange de gaz idéaux se comporte lui-même comme un gaz idéal.
La composition d’un mélange est généralement déterminée à partir soit des fractions molaires, soit des fractions massiques des constituants. Dans cette section, nous établirons les expressions des diverses grandeurs thermodynamiques usuelles en fonction de ces grandeurs.
Fractions molaires et fractions massiques
Le nombre total de moles n du mélange est égal à la somme des nombres moles des divers constituants :
n = n1 + n2 + n3 + ... nn =
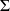 ni
ni
La fraction molaire d'un constituant est par définition le rapport du nombre de moles de ce constituant au nombre total de moles dans le mélange :
xi = ni/n et
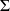 xi = 1
xi = 1
Par ailleurs, la loi de conservation de la masse implique que la masse totale est égale à la somme des masses des constituants :
m = m1 + m2 + m3 + ... mn =
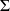 mi
mi
La fraction massique d'un constituant est par définition le rapport de la masse de ce constituant à la masse totale du mélange :
yi = mi/m et
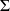 yi = 1
yi = 1
Loi de Dalton des gaz idéaux
On définit la pression partielle Pi d'un constituant comme étant la pression qu'exercerait ce constituant s'il occupait seul le volume V du mélange, sa température étant égale à celle du mélange.
La loi de Dalton postule que la pression, l'énergie interne, l'enthalpie et l'entropie d'un mélange de gaz idéaux à la température T et à la pression P sont respectivement la somme des pressions, des énergies internes, des enthalpies et des entropies partielles des gaz constituants, c'est-à-dire pris séparément à la température T et à leur pressions partielles.
Chaque constituant se comporte donc comme s'il existait à la température T du mélange et occupait seul le volume V.
Physiquement, cela signifie que les champs de forces moléculaires des différents constituants n'interfèrent pas entre eux.
Mathématiquement, la loi de Dalton se traduit par les deux lois suivantes, P étant la pression totale :
Pi = xi P (10)
cp = 1/m
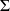 cpi mi =
cpi mi =
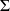 yi cpi (11)
yi cpi (11)
La capacité thermique massique à pression constante du mélange est égale à la somme des produits des capacités thermiques massiques des constituants par leurs fractions massiques.
La loi de Dalton signifie qu'un mélange de gaz idéaux se comporte lui-même comme un gaz idéal, dont la mole fictive aurait une masse molaire M =
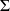 xi Mi.
xi Mi.
Elle a pour conséquence que les résultats établis pour les gaz idéaux peuvent être utilisés pour calculer les évolutions des mélanges de ces gaz, ce qui est d'une importance capitale en pratique.
On a : yi = xi Mi/M
On peut aussi définir une constante équivalente des gaz idéaux par :
r = R/M (kJ/kg/K)
En notations massiques, la constante des gaz idéaux du mélange s’exprime sous une forme très simple :
r =
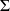 yi ri (12)
yi ri (12)
Par ailleurs, H =
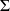 Hi et m cp T =
Hi et m cp T =
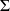 cpi mi T
cpi mi T
On en déduit (11).
En notations molaires, (11) devient :
Cp =
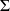 xi Cpi (13)
xi Cpi (13)
Propriétés énergétiques des mélanges de gaz idéaux
Enthalpie d'un mélange
Selon la loi de Dalton, l'enthalpie d'un mélange de gaz idéaux est égale à la somme des enthalpies de chacun des constituants.
notations massiques : h =
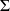 yi hi (14)
yi hi (14)notations molaires : H =
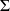 xi Hi (15)
xi Hi (15)
Le calcul de l'énergie interne se ferait de la même manière.
Entropie d'un mélange
C'est pour le calcul de l'entropie du mélange qu'apparaît la signification profonde de la loi de Dalton, selon laquelle la valeur de l'entropie du mélange doit être calculée en sommant les entropies des constituants pris à la température T et à leurs pressions partielles Pi.
En effet, l'entropie du mélange est supérieure à la somme des entropies des constituants avant mélange d’une valeur km = - r
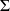 xi ln xi > 0. Physiquement, ceci s'explique par le
caractère irréversible de l'opération de mélange. Il importe de remarquer que l'écart km reste une constante (indépendante de T et de P) tant que les concentrations ne varient pas. Cet écart doit être pris en compte une fois pour toutes lors du calcul de l'entropie de référence, mais ensuite, le mélange se comportant lui même comme un gaz idéal, on n'a plus à s'en soucier.
xi ln xi > 0. Physiquement, ceci s'explique par le
caractère irréversible de l'opération de mélange. Il importe de remarquer que l'écart km reste une constante (indépendante de T et de P) tant que les concentrations ne varient pas. Cet écart doit être pris en compte une fois pour toutes lors du calcul de l'entropie de référence, mais ensuite, le mélange se comportant lui même comme un gaz idéal, on n'a plus à s'en soucier.
Bien entendu ceci ne reste plus vrai si la composition du mélange vient à varier au cours de la transformation, auquel cas il faut calculer les différentes valeurs de km pour déterminer les variations d'entropie.
Thermoptim utilise deux catégories de gaz idéaux :
les gaz purs, dont les propriétés sont prédéterminées dans le progiciel, et non modifiables par l'utilisateur. Ils sont au nombre de 20 environ ;
les gaz composés, construits par l'utilisateur à son gré à partir des gaz purs compris dans la base. Leurs propriétés sont calculées par le progiciel par application de la loi de Dalton.
Parmi eux, on distingue les gaz composés protégés des autres, non protégés. Cette distinction tient simplement à ce que la composition d'un gaz composé protégé ne peut pas être modifiée par le progiciel, afin qu'une erreur de modélisation ne puisse la changer.
A titre d'exemple, le gaz "air" qui correspond à l'air sec est un gaz composé protégé dont la composition reste invariable.
