Exergie
EXERGIE
La théorie de l'exergie a pour objet de développer une méthode d'analyse intégrée qui englobe les deux premiers principes de la thermodynamique, et permette ainsi de tenir compte à la fois des quantités d'énergie mises en jeu et de leur qualité, ce que le premier principe ne permet pas de faire. Son intérêt est qu'elle fournit un cadre tout à fait rigoureux pour quantifier la qualité thermodynamique d'un système quelconque, ouvert ou fermé, en régime dynamique ou non.
Le premier à avoir introduit cette notion est G. Gouy, qui, à la fin du XIXe siècle, a défini la notion d'énergie utilisable, aujourd'hui rebaptisée exergie par de nombreux auteurs. L'idée de base est de considérer qu'un système thermodynamique interagit avec son environnement, lequel se comporte comme un réservoir infini à température[1] et pression constantes et de composition fixée, ce qui signifie que le système étudié est suffisamment petit devant cet environnement pour ne pas le perturber.
Cet environnement servira par exemple de source froide pour un cycle moteur, ou de source chaude pour un cycle de réfrigération. Étant donné que l'état de l'environnement conditionne les performances du système étudié, la théorie de l'exergie permet d'en tenir compte implicitement lorsqu'on cherche à les calculer.
Dans le cadre de cette page, nous nous contenterons d'une présentation succincte (et donc non rigoureuse) et en régime permanent de l'analyse exergétique. Le lecteur désireux de s'engager plus à fond dans cette voie trouvera notamment dans l'ouvrage de L. Borel et D. Favrat cité en référence une théorie complète du sujet.
Précisons aussi qu'une séance Diapason est consacrée à la notion d'exergie et à l'établissement des bilans exergétiques, ainsi qu'une rubrique des Guides méthodologiques du portail.
PRÉSENTATION DE L'EXERGIE POUR UN SYSTÈME MONOTHERME OUVERT EN RÉGIME PERMANENT
Soit un système ouvert[2] fonctionnant en régime permanent échangeant de l'énergie avec son environnement supposé à température[1] uniforme T0 (figure ci-dessous).
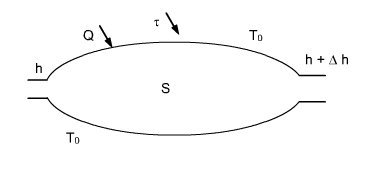
L'équation énergétique est donnée par le premier principe :
Δh + ΔK =
 + Q
+ Q
et la production d'entropie par le deuxième principe :
Q +
 = T0 Δs , avec 0
= T0 Δs , avec 0
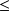

Δs - Q/T0
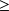 0
0
Si l'on fait l'hypothèse que toute la chaleur est fournie par l'environnement, et que T0 est la température à la frontière du système ouvert[2], on peut éliminer Q en combinant ces deux équations, ce qui donne :
 = Δh + ΔK - Q
= Δh + ΔK - Q
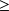 Δh + ΔK - T0Δs
Δh + ΔK - T0Δs
-

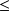 - (Δh + ΔK - T0Δs)
- (Δh + ΔK - T0Δs)
Dans la plupart des cas, on peut négliger les variations d'énergie cinétique ΔK.
Pour un système ouvert[2], on appelle généralement exergie la fonction xh = h - T0 s.
Le travail maximum que peut fournir le système est égal à la diminution de son exergie.
En pratique, le travail réel fourni par le système peut être inférieur à cette valeur. On définit la perte exergétique Δxhi, comme étant égale à la différence entre le travail maximum possible et le travail réel fourni :
Δxhi = (-
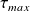 ) - (-
) - (-
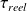 ) = (-Δxh) - (-
) = (-Δxh) - (-
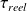 )
)
Δxhi = T0Δs - Δh - (-
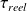 )
)
Si le processus est de plus adiabatique,
(-
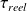 ) = - Δh et Δxhi = - Δxh + Δh = T0Δs
) = - Δh et Δxhi = - Δxh + Δh = T0Δs
On notera que cette dénomination n'est pas parfaitement satisfaisante, car on voit bien que, pour un système fermé[2], la définition de l'exergie amène à considérer la fonction u - T0s, de telle sorte que l'on est en présence d'une ambiguïté. C'est pourquoi L. Borel et D. Favrat proposent de parler plutôt de coenthalpie et de coénergie.
Au delà de la question du vocabulaire, on remarquera que cette nouvelle fonction se caractérise par l'introduction d'une grandeur extérieure au système, T0. A ce titre, ce n'est plus une fonction d'état[3] au sens strict. Toutefois, comme T0 est généralement supposée constante, l'exergie est quelquefois présentée comme une combinaison linéaire de fonctions d'état.
Une autre remarque peut être faite à ce stade : l'exergie permet, par le biais de la multiplication de l'entropie par la température de l'environnement, d'exprimer les variations de cette fonction d'état[4] dans une dimension et par des ordres de grandeur comparables à ceux auxquels l'ingénieur est habitué lorsqu'il fait des calculs énergétiques, ce qui facilite la compréhension physique des phénomènes considérés.
Enfin, comme nous le verrons ci-dessous, on réussit par cet artifice à éliminer formellement des calculs la source de chaleur "gratuite" représentée par l'environnement.
L'exergie permet d'évaluer la qualité des transformations réalisées dans les processus réels, par rapport aux évolutions idéales réversibles.
SYSTÈME OUVERT MULTITHERME EN RÉGIME PERMANENT
Soit un système ouvert qui échange du travail et de la chaleur avec n sources extérieures à températures constantes Tk, et l'environnement pris à la température T0 (figure ci-dessous).
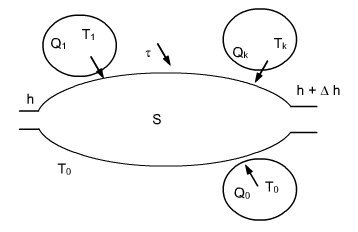
L’application du premier principe donne ici :
Δh + ΔK =
 + Q0 +
+ Q0 +
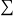 Qk
Qk
et la production d'entropie est donnée par le deuxième principe
Δs = Q0/T0+
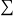 Qk/Tk+ Δsi
Qk/Tk+ Δsi
Δsi, positif ou nul, étant la génération d'entropie. En négligeant les variations d’énergie cinétique, il vient :
Δxh = Δ(h - T0 s) =
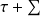 (1-T0/Tk)Qk - T0 Δsi (1)
(1-T0/Tk)Qk - T0 Δsi (1)
ou encore, posant Δxhi = T0 Δsi
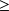 0:
0:
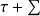 (1-T0/Tk)Qk - Δxh - Δxhi = 0 (2)
(1-T0/Tk)Qk - Δxh - Δxhi = 0 (2)
 représente le travail reçu par le système, Δxh la variation d’exergie du fluide qui le traverse, et Δxhi la dissipation d'exergie résultant des irréversibilités. On appelle facteur de Carnot le terme
représente le travail reçu par le système, Δxh la variation d’exergie du fluide qui le traverse, et Δxhi la dissipation d'exergie résultant des irréversibilités. On appelle facteur de Carnot le terme
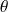 = 1 - T0/T. Il s’agit du facteur par lequel il faut multiplier une quantité Q de chaleur disponible à une température T pour obtenir la valeur de son exergie. Si on appelle exergie-chaleur la quantité xq =
= 1 - T0/T. Il s’agit du facteur par lequel il faut multiplier une quantité Q de chaleur disponible à une température T pour obtenir la valeur de son exergie. Si on appelle exergie-chaleur la quantité xq =
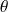 Q, l’équation (2) se met sous la forme :
Q, l’équation (2) se met sous la forme :
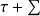
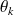 Qk - Δxh - Δxhi = 0
Qk - Δxh - Δxhi = 0
-
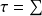 xqk - Δxh - Δxhi (3)
xqk - Δxh - Δxhi (3)
Le travail moteur maximum que peut fournir un système ouvert est égal à la somme des exergies-chaleurs des sources avec lesquelles il échange de la chaleur, diminuée de la variation d’exergie du fluide qui le traverse et de l’exergie détruite du fait des irréversibilités.
APPLICATION À UNE MACHINE DITHERME RÉVERSIBLE
Soit une machine ditherme réversible cyclique fonctionnant entre une source à la température T1 et l'environnement à température T0. Sur un cycle, on a : Δxh = 0 , Δxhi = 0 (machine réversible)
L’application de la formule (3) donne : -
 = xq1 = (1 - T0/T1) Q1
= xq1 = (1 - T0/T1) Q1
Si T0 < T1, xq1
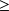 0 ; le système reçoit de l'exergie-chaleur de la source chaude à T1, et la convertit en travail
0 ; le système reçoit de l'exergie-chaleur de la source chaude à T1, et la convertit en travail
 .
.
On retrouve ici le cycle de Carnot, d'efficacité
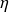 = 1 - T0/T1.
= 1 - T0/T1.
Si T0 > T1, xq1
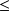 0 ; le système cède de l'exergie-chaleur à la source froide à T1, en la prenant à la source chaude à T0. Pour cela, il faut lui fournir un travail
0 ; le système cède de l'exergie-chaleur à la source froide à T1, en la prenant à la source chaude à T0. Pour cela, il faut lui fournir un travail
 . Il s'agit alors d'une frigopompe.
. Il s'agit alors d'une frigopompe.
CAS PARTICULIER : ÉCHANGES THERMIQUES SANS PRODUCTION DE TRAVAIL
Dans le cas particulier où il n’y a pas de production de travail, l’équation (3) peut se réécrire :
Δxhi =
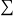 xqk- Δxh (4)
xqk- Δxh (4)
L’exergie détruite dans le processus est égale à la somme des exergies-chaleurs des différentes sources, diminuée de la variation d’exergie du fluide qui traverse le système.
RENDEMENT EXERGÉTIQUE
L'exergie permet de définir rigoureusement la notion de rendement d'une installation, et donc de quantifier sa qualité thermodynamique : c'est le rapport des utilisations exergétiques aux ressources exergétiques. Il est toujours compris entre 0 et 1, et d'autant plus élevé que les irréversibilités sont faibles. Les ressources exergétiques correspondent à la somme de toutes les exergies que l'on a dû fournir au cycle en provenance de l'extérieur. Les utilisations exergétiques représentent le bilan net du cycle, c'est-à-dire la somme algébrique des exergies produites et consommées en son sein.
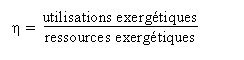
REFERENCES
A. BEJAN, G. TSATSARONIS, M. MORAN, Thermal design and optimization, Wiley publishers, 1996.
L. BOREL, D. FAVRAT, Thermodynamique et énergétique, Presses Polytechniques Romandes, Lausanne, Vol. 1 (De l'énergie à l'exergie), 2005, Vol. 2 (Exercices corrigés), 1987.
